初中数学解直角三角形试题

如图，在矩形ABCD中，AB=4，AD=5，P是射线BC上的一个动点，过点P作PE⊥AP，交射线DC于点E，射线AE交射线BC于点F，设BP=a．

（1）当点P在线段BC上时（点P与点B，C都不重合），试用含a的代数式表示CE；
（2）当a=3时，连结DF，试判断四边形APFD的形状，并说明理由；
（3）当tan∠PAE=时，求a的值．

如图，在平面直角坐标系中，的外接圆与轴交于点，，求的长．

如图，AB是⊙O的直径，弦CD⊥AB于点H，点G在弧BD上，连接AG，交CD于点K，过点G的直线交CD延长线于点E，交AB延长线于点F，且EG=EK．

（1）求证：EF是⊙O的切线；
（2）若⊙O的半径为13，CH=12，AC∥EF，求OH和FG的长．

如图，在△ABC中，∠B=90°，∠ACB=60°，AB=，AD⊥AC，连接CD.点E在AC上，，过点E作MN⊥AC，分别交AB、CD于点M、N.

（1）求ME的长；
（2）当AD=3时，求四边形ADNE的周长.

如图，在平面直角坐标系中，Rt△OAB的顶点A的坐标为（9，0),，点C的坐标为（2，0），点P为斜边OB上的一个动点，则PA+PC的最小值为_______________.

由于2013年第30号强台风“海燕”的侵袭,致使多个城市受到影响. 如图所示,A市位于台风中心M北偏东15°的方向上,距离千米,B市位于台风中心M正东方向千米处. 台风中心以每小时30千米的速度沿MF向北偏东60°的方向移动（假设台风在移动的过程中的风速保持不变）,距离台风中心60千米的圆形区域内均会受到此次强烈台风的影响.

（1）A市、B市是否会受到此次台风的影响？说明理由.
（2）如果受到此次台风影响,该城市受到台风影响的持续时间为多少小时?

如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，DE＝3，连接DB，过点E作EM∥BD，交BA的延长线于点M．

（1）求⊙O的半径；
（2）求证：EM是⊙O的切线；
（3）若弦DF与直径AB相交于点P，当∠APD＝45º时，求图中阴影部分的面积．

已知：△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.

（1）求证：直线EF是⊙O的切线；
（2）当直线DF与⊙O相切时,求⊙O的半径.

如图，在△ABC中，AB=AC，以AC为直径的半圆O交BC于点E，DE⊥AB，垂足为D．

（1）求证：点E是BC的中点；
（2）判断DE与⊙O的位置关系，并证明你的结论；
（3）如果⊙O的直径为9，cosB=，求DE的长．

如图,已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16海里,一艘货轮从B港口以40海里/h的速度沿∠ABC=45°的BC方向航行.现测得C处位于Ａ观测点北偏东79.8°（即∠DAC=79.8°）方向.求此时货轮C与AB之间的最近距离（精确到0.1海里）.

(参考数据：sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,)

如图，AD是△ABC的角平分线，以点C为圆心，CD为半径作圆交BC的延长线于点E，交AD于点F，交AE于点M，且∠B=∠CAE，EF：FD=4：3．

（1）求证：点F是AD的中点；
（2）求cos∠AED的值；
（3）如果BD=10，求半径CD的长．

如图，AB为⊙O的直径，点C在⊙O上，点P是直径AB上的一点，（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q.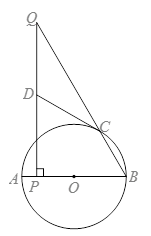

（1）点D在线段PQ上，且DQ=DC.求证：CD是⊙O的切线；
（2）若sinQ=，BP=6，AP=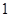，求QC的长.

如图，和都是以A为直角顶点的等腰直角三角形，连结BD，BE，CE，延长CE交AB于点F，交BD于点G．

（1）求证：；
（2）若是边长可变化的等腰直角三角形，并将绕点旋转，使CE的延长线始终与线段BD（包括端点B、D）相交．当为等腰直角三角形时，求出的值．

如图，△ABC中，AB=5，BC=11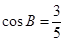，，点P是BC边上的一个动点，联结AP，取AP的中点M，将线段MP绕点P顺时针旋转90°得到线段PN，联结AN，NC.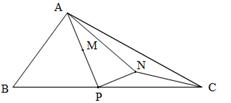

（1）当点N恰好落在BC边上时，求NC的长；
（2）若点N在△ABC内部（不含边界），设BP=x，CN=y，求y关于x的函数关系式，并求出函数的定义域；
（3）若△PNC是等腰三角形，求BP的长.

已知A（，0），直线与x轴交于点F，与y轴交于点B，直线l∥AB且交y轴于点C，交x轴于点D，点A关于直线l的对称点为A′，连接AA′、A′D．直线l从AB出发，以每秒1个单位的速度沿y轴正方向向上平移，设移动时间为t．

（1）求点A′的坐标（用含t的代数式表示）；
（2）求证：AB＝AF；
（3）过点C作直线AB的垂线交直线于点E，以点C为圆心CE为半径作⊙C，求当t为何值时，⊙C与△AA′D三边所在直线相切？