初中数学解直角三角形试题

已知梯形ABCD中，AD∥BC，AB=15，CD=13，AD=8，∠B是锐角，∠B的正弦值为，那么BC的长为       ．

如图，AB是⊙O的直径，点A、C、D在⊙O上，BP是⊙O的切线，连接PD并延长交⊙O于F、交AB于E，若∠BPF=∠ADC.

（1）判断直线PF与AC的位置关系，并说明你的理由；
（2）当⊙O的半径为5，tan∠P=，求AC的长.

如图，已知在Rt△ABC中，∠ACB=90°，AB=10,tanA=4/3,点D是斜边AB上的动点，连接CD，作DE⊥CD，交射线CB于点E,设AD=x。（1）当点D是边AB的中点时，求线段DE的长；（2）当△BED是等腰三角形时，求x的值；（3）如果y=DE/DB。求y关于x的函数解析式，并写出它的定义域。

在中，，，，以AB为一边作等腰直角三角形ABD，使，连结CD，则线段CD的长为__________.

已知：如图，在等腰直角△ABC中，AC=BC，斜边AB的长为4，过点C作射线CP//AB，D为射线CP上一点，E在边BC上（不与B、C重合），且∠DAE=45°，AC与DE交于点O．

（1）求证：△ADE∽△ACB；
（2）设CD=x，BAE = y，求y关于x的函数解析式，并写出它的定义域；
（3）如果△COD与△BEA相似，求CD的值．

小华同学学习了第二十五章《锐角三角比》后，对求三角形的面积方法进行了研究，得到了新的结论：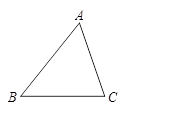

（1）如图1，已知锐角△ABC．求证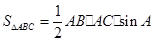：；（2）根据题（1）得到的信息，请完成下题：如图2，在等腰△ABC中，AB=AC=12厘米，点P从A点出发，沿着边AB移动，点Q从C点出发沿着边CA移动，点Q的速度是1厘米/秒，点P的速度是点Q速度的2倍，若它们同时出发，设移动时间为t秒，问：当t为何值时，?

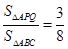如图，点G是Rt△ABC的重心，过点G作矩形GECF，当GF：GE=1：2时，则∠ B的正切值为   ．

如图，BC是⊙O的直径，A是⊙O上一点，过点C作⊙O的切线，交BA的延长线于点D，取CD的中点E，AE的延长线与BC的延长线交于点P。

（1）求证：AP是⊙O的切线；
（2）若OC＝CP，AB＝，求CD的长。

如图，∠ACB＝60°，半径为2的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离为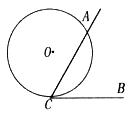

A．4

B．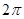

C．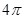

D．

在半径为1的⊙O中，弦AB的长为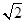，则弦AB所对的圆周角的度数为

A．45°

B．60°

C．45°或135°

D．60°或120°

已知：如图所示，AB是⊙的弦，，C是优弧AB上的一点，BD//OA，交CA的延长线于点D，连接BC。

（1）求证：BD是⊙的切线；
（2）若，求⊙的半径。

如图，已知抛物线与x轴交于A、B两点，点C是抛物线在第一象限内部分的一个动点，点D是OC的中点，连接BD并延长，交AC于点E.

（1）说明：；
（2）当点C、点A到y轴距离相等时，求点E坐标.
（3）当的面积为时，求的值.

如图，在平行四边形ABCD中，AD＝5cm， AP＝8cm， AP平分∠DAB，交DC于点P，过点B作BE⊥AD于点E，BE交AP于点F，则tan∠BFP＝        ．

已知二次函数y=x²﹣2mx+4m﹣8（1）当x≤2时，函数值y随x的增大而减小，求m的取值范围．（2）以抛物线y=x²﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN（M，N两点在拋物线上），请问：△AMN的面积是与m无关的定值吗？若是，请求出这个定值；若不是，请说明理由．（3）若抛物线y=x²﹣2mx+4m﹣8与x轴交点的横坐标均为整数，求整数m的最小值．

如图，直径为10的⊙A经过点C(0,5)和点O (0,0)，B是y轴右侧⊙A优弧上一点,则∠OBC 的正弦值为                ．