初中数学解直角三角形试题

如图，半径为6cm的⊙O中，C，D为直径AB的三等分点，点E，F分别在AB两侧的半圆上，∠BCE=∠BDF=60°，连结AE，BF，则图中两个阴影部分的面积为   cm²

如图，AB是⊙O的直径，点C，D是半圆O的三等分点，过点C作⊙O的切线交AD的延长线于点E，过点D作DF⊥AB于点F，交⊙O于点H，连接DC，AC．
（1）求证：∠AEC=90°；
（2）试判断以点A，O，C，D为顶点的四边形的形状，并说明理由；
（3）若DC=2，求DH的长．

在一次科技活动中，小明进行了模拟雷达雪描实验.如图，表盘是△ABC，其中AB=AC，∠BAC=120°，在点A处有一束红外光线AP，从AB开始，绕点A逆时针匀速旋转，每秒钟旋转15°，到达AC后立即以相同的旋转速度返回A、B，到达后立即重复上述旋转过程.小明通过实验发现，光线从AB处开始旋转计时，旋转1秒， 时光线AP交BC于点M，BM的长为（）cm.
（1）求AB的长；
（2）从AB处旋转开始计时，若旋转6秒，此时AP与BC边交点在什么位置？若旋转2014秒，此时AP与BC边交点在什么位置？并说明理由.

如图，等腰△ABC中，AB=AC，∠BAC=36°，BC=1，点D在边AC上且BD平分∠ABC，设CD=x．
（1）求证：△ABC∽△BCD；
（2）求x的值；
（3）求cos36°-cos72°的值．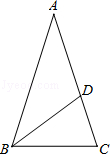

如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上,∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC.
(1) 试判断BE与FH的数量关系，并说明理由；
(2) 求证：∠ACF=90°；
(3) 连接AF，过A，E，F三点作圆，如图2. 若EC=4，∠CEF=15°，求的长.

图1                         图2

△ABC为等边三角形，边长为a，DF⊥AB，EF⊥AC，
（1）求证：△BDF∽△CEF；
（2）若a=4，设BF=m，四边形ADFE面积为S，求出S与m之间的函数关系，并探究当m为何值时S取最大值；
（3）已知A、D、F、E四点共圆，已知tan∠EDF=，求此圆直径．

在矩形ABCD中，，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．
（1）如图1，当DH=DA时，
①填空：∠HGA=       度；
②若EF∥HG，求∠AHE的度数，并求此时a的最小值；
（2）如图3，∠AEH=60°，EG=2BG，连接FG，交边FG，交边DC于点P，且FG⊥AB，G为垂足，求a的值．

如图，抛物线y=﹣x²+3x+4与x轴交于A、B两点，与y轴交于C点，点D在抛物线上且横坐标为3．
（1）求tan∠DBC的值；
（2）点P为抛物线上一点，且∠DBP=45°，求点P的坐标．

如图（1），在平面直角坐标系中，点A（0，﹣6），点B（6，0）．Rt△CDE中，∠CDE=90°，CD=4，DE=4，直角边CD在y轴上，且点C与点A重合．Rt△CDE沿y轴正方向平行移动，当点C运动到点O时停止运动．解答下列问题：
（1）如图（2），当Rt△CDE运动到点D与点O重合时，设CE交AB于点M，求∠BME的度数．
（2）如图（3），在Rt△CDE的运动过程中，当CE经过点B时，求BC的长．
（3）在Rt△CDE的运动过程中，设AC=h，△OAB与△CDE的重叠部分的面积为S，请写出S与h之间的函数关系式，并求出面积S的最大值．

如图，AB是⊙O的直径，C是⊙O上的一点，过点A作AD⊥CD于点D，交⊙O于点E，且=．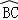
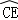（1）求证：CD是⊙O的切线；
（2）若tan∠CAB=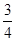，BC=3，求DE的长．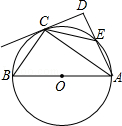

阅读下面材料：
小腾遇到这样一个问题：如图1，在中，点在线段上，，，，，求的长．

小腾发现，过点作，交的延长线于点，通过构造，经过推理和计算能够使问题得到解决（如图2）．
请回答：的度数为         ，的长为            ．
参考小腾思考问题的方法，解决问题：
如图3，在四边形中，，，，与交于点，，，求的长．

将两块全等的三角板如图①摆放，其中∠A₁CB₁=∠ACB=90°，∠A₁=∠A=30°．
（1）将图①中的△A₁B₁C顺时针旋转45°得图②，点P₁是A₁C与AB的交点，点Q是A₁B₁与BC的交点，求证：CP₁=CQ；
（2）在图②中，若AP₁=2，则CQ等于多少？
（3）如图③，在B₁C上取一点E，连接BE、P₁E，设BC=1，当BE⊥P₁B时，求△P₁BE面积的最大值．

阅读下面材料：
在学习小组活动中，小明探究了下面问题：菱形纸片ABCD的边长为2，折叠菱形纸片，将B、D两点重合在对角线BD上的同一点处，折痕分别为EF、GH．当重合点在对角线BD上移动时，六边形AEFCHG的周长的变化情况是怎样的？
小明发现：若∠ABC=60°，
①如图1，当重合点在菱形的对称中心O处时，六边形AEFCHG的周长为_________；
②如图2，当重合点在对角线BD上移动时，六边形AEFCHG的周长_________（填“改变”或“不变”）.
请帮助小明解决下面问题：
如果菱形纸片ABCD边长仍为2，改变∠ABC的大小，折痕EF的长为m．
（1）如图3，若∠ABC=120°，则六边形AEFCHG的周长为_________；
（2）如图4，若∠ABC的大小为，则六边形AEFCHG的周长可表示为________．

如图，在△ABC中，∠ACB=90º，∠ABC=30º，BC=，以AC为边在△ABC的外部作等边△ACD，连接BD．
（1）求四边形ABCD的面积；
（2）求BD的长．

如图，所有正三角形的一边平行于x轴，一顶点在y轴上．从内到外，它们的边长依次为2,4,6,8，…，顶点依次用表示，其中x轴与边，边与，与，…均相距一个单位，则顶点的坐标为       ；的坐标为         ；（n为正整数）的坐标为         ．