如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.
(1)求证:△CDF≌△CBE.
(2)若CD=8.EF=10 .求∠DCF的余弦值.
.求∠DCF的余弦值.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN= 
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米。某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°。
(1)沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;
(2)由于海流原因,“蛟龙”号需在B点处马上上浮,若平均垂直上浮速度为2000米/时,求“蛟龙”号上浮回到海面的时间。(参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
如图,点A、B、C分别是⊙O上的点,CD是⊙O的直径,P是CD延长线上的一点,AP=AC.
(1)若∠ABC=60°.求证:AP是⊙O的切线;
(2)若点B是弧CD的中点,AB交CD于点E,CD=4,求BE•AB的值.
已知,如图,在笔山银子岩坡顶A处的同一水平面上有一座移动信号发射塔BC,笔山职中数学兴趣小组的同学在斜坡底P处测得该塔的塔顶B的仰角为45°,然后他们沿着坡度为1:2.4的斜坡AP攀行了26米,在坡顶A处又测得该塔的塔顶B的仰角为76°.求: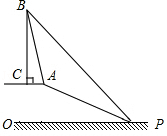
(1)坡顶A到地面PO的距离;(2)移动信号发射塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
在中俄“海上联合—2014”反潜演习中,我军舰A测得潜艇C的俯角为300.位于军舰A正上方1000米的反潜直升机B侧得潜艇C的俯角为680,试根据以上数据求出潜艇C离开海平面的下潜深度。(结果保留整数。参考数据:sin680≈0.9,cos680≈0.4,,tan680≈2.5. ≈1.7)
≈1.7)
如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果 ,
, .那么m与n满足的关系式是:m= (用含n的代数式表示m).
.那么m与n满足的关系式是:m= (用含n的代数式表示m).
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,且BF是⊙O的切线,BF交AC的延长线于F.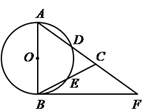
(1)求证:∠CBF=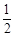 ∠CAB. (2)若AB=5,sin∠CBF=
∠CAB. (2)若AB=5,sin∠CBF=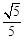 ,求BC和BF的长.
,求BC和BF的长.
如图,在四边形ABCD中,AC平分∠DAB,CE⊥AB于E.
(1)若AB=AD+2BE,求证:BC=DC;
(2)若∠B=60°,AC=7,AD=6, ,求AB的长.
,求AB的长.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,BE=1,求cosA的值.
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66°.
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度l(即AD+AB+BC,结果精确到0.1米).(参考数据:sin66°≈0.91,cos66°≈0.41,tan66°≈2.25,cot66°≈0.45)
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
问题探究(本题10分):
(1)请在图①的正方形ABCD内,画出使∠APB=90°的一个点,并说明理由.
(2)请在图②的正方形ABCD内(含边),画出使∠APB=60°的所有的点P,
并说明理由.
问题解决:
(3)如图③,现在一块矩形钢板ABCD,AB=4,BC=3.工人师傅想用它
裁出两块全等的.面积最大的△APB和△CP'D钢板,且∠APB=∠CP'D=60°.
请你在图③中画出符合要求的点和P和P'.
如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点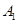 处,已知OA=
处,已知OA=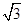 ,AB=1,则点
,AB=1,则点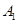 的坐标是( )
的坐标是( )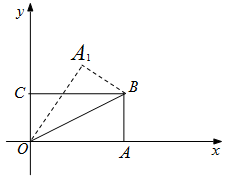
A.(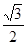 , ,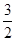 ) ) |
B.(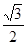 ,3) ,3) |
C.(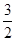 , ,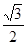 ) ) |
D.(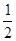 , ,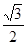 ) ) |