初中数学解直角三角形试题

2015年4月25日14时11分尼泊尔发生了8．1级大地震．山坡上有一棵与水平面垂直的大树，大地震过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面（如图所示）．已知山坡的坡角∠AEF=23°，量得树干的倾斜角为∠BAC=38°，大树被折断部分和坡面所成的角∠ADC=60°，AD=4米．

（1）求∠DAC的度数；
（2）求这棵大树原来的高度是多少米？（结果精确到个位，参考数据：，，）

某水库大坝的横截面是如图所示的四边形BACD，期中AB∥CD．瞭望台PC正前方水面上有两艘渔船M、N，观察员在瞭望台顶端P处观测渔船M的俯角，观测渔船N在俯角，已知NM所在直线与PC所在直线垂直，垂足为点E，PE长为30米．
（1）求两渔船M，N之间的距离（结果精确到1米）；
（2）已知坝高24米，坝长100米，背水坡AD的坡度．为提高大坝防洪能力，某施工队在大坝的背水坡填筑土石方加固，加固后坝定加宽3米，背水坡FH的坡度为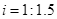，施工12天后，为尽快完成加固任务，施工队增加了机械设备，工作效率提高到原来的1．5倍，结果比原计划提前20天完成加固任务，施工队原计划平均每天填筑土石方多少立方米？（参考数据：）

如图1为两个边长为1的正方形组成的格点图,点A,B,C,D都在格点上,AB,CD交于点P,则tan∠BPD=     ,如果是n个边长为1的正方形组成的格点图,如图2,那么tan∠BPD=     ．

如图1，△ABC中，AB=AC，点D在BA的延长线上，点E在BC上，DE=DC，点F是DE与AC的交点，且DF=FE．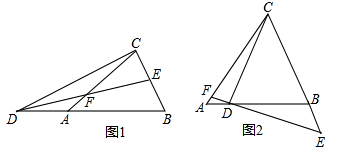

（1）图1中是否存在与∠BDE相等的角？若存在，请找出，并加以证明，若不存在，说明理由；
（2）求证：BE=EC；
（3）若将“点D在BA的延长线上，点E在BC上”和“点F是DE与AC的交点，且DF=FE”分别改为“点D在AB上，点E在CB的延长线上”和“点F是ED的延长线与AC的交点，且DF=kFE”，其他条件不变（如图2）．当AB=1，∠ABC=a时，求BE的长（用含k、a的式子表示）．

公园中有一棵树和一座塔恰好座落在一条笔直的道路上．在途中A处，小杰测得树顶和塔尖的仰角分别为45º和30º，继续前进8米至B处，又测得树顶和塔尖的仰角分别为16º和45º，试问这棵树和这座塔的高度分别为多少米？（结果精确0．1米．参考数据：≈1．414，≈1．732，tan16º≈0．287，sin16º≈0．276，cos16º≈0．961）

如图，在△中，∠的垂直平分线交AB于点D，交的延长线于点，则的长为（   ）

A．

B．

C．

D．

如图，小山的顶部是一块平地，在这块平地上有一高压输电的铁架，小山的斜坡的坡度，斜坡BD的长是50米，在山坡的坡底B处测得铁架顶端A的仰角为45°，在山坡的坡顶D处测得铁架顶端A的仰角为．

（1）求小山的高度；
（2）求铁架的高度．

小明坐于堤边垂钓，如图，河堤AC的坡角为30°，AC长米，钓竿AO的倾斜角是60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离．

如图，点A，B，C表示某旅游景区三个缆车站的位置，线段AB，BC表示连接缆车站的钢缆，已知A，B，C三点在同一铅直平面内，它们的海拔高度AA′，BB′，CC′分别为110米、310米、710米，钢缆AB的坡度i1=1：2，钢缆BC的坡度i2=1：1．景区因改造缆车线路，需要从A到C直线架设一条钢缆，那么钢缆AC的长度是多少米？（注：坡度是指坡面的铅直高度与水平宽度的比．）

（1）如图①，若BC=6，AC=4，∠C=60°，求△ABC的面积S_△ABC；
（2）如图②，若BC=a，AC=b，∠C=α，求△ABC的面积S_△ABC；
（3）如图③，四边形ABCD，若AC=m，BD=n，对角线AC、BD交于O点，它们所成的锐角为β．求四边形ABCD的面积S_{四边形ABCD} ．

如图，在四边形ABCD中，E、F分别是AB、AD的中点．若EF=2，BC=5，CD=3，则tanC等于（      ）

A．             B．           C．          D．

如图1，在△ABC中，∠ACB=90°，∠CAB=30°， △ABD是等边三角形，E是AB的中点，连结CE并延长交AD于F，如图2，现将四边形ACBD折叠，使D与C重合，HK为折痕，则sin∠ACH的值为（  ）

A．

B．

C．

D．

如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BFQ＝60°，EF＝1km．

（1）判断线段AB与AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）．

海中两个灯塔A、B，其中B位于A的正东方向上，渔船跟踪鱼群由西向东航行，在点C处测得灯塔A在西北方向上，灯塔B在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D，这是测得灯塔A在北偏西60°方向上，求灯塔A、B间的距离．（计算结果用根号表示，不取近似值）

如图，在平面直角坐标系中，二次函数的图象与一次函数的图象交于A、B两点，点A在x轴上，点B的纵坐标为．点P是二次函数图象上A、B两点之间的一个动点（不与点A、B重合），设点P的横坐标为m，过点P作x轴的垂线交AB于点C，作PD⊥AB于点D．

（1）求b及sin∠ACP的值；
（2）用含m的代数式表示线段PD的长；
（3）连接PB，线段PC把△PDB分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为．如果存在，直接写出m的值；如果不存在，请说明理由．