如图,两建筑物的水平距离BC是30m,从A点测得D点的俯角α是35°,测得C点的俯角β为43°,求这两座建筑物的高度。(结果保留整数)
李萌“五一”假到恩施州利川市齐岳山风电场游玩,看见风电场的各个山头上布满了大大小小的风力发电机,好奇地想知道风扇叶片的长度大约是多少米?如图1是其中的一个风力发电机图片,图2是其根据风力发电机所处的地理位置抽象出的几何图形.几何图形中OA是风力发电机离水平线AB的垂直高度,三个相同的风扇叶片随风绕O点顺时针方向不停地旋转,OC是其中一个叶片的长度,A、B在同一水平线上,李萌在点B处进行测量,测得 AB=60米,当叶片OC旋转到最高处时(A、O、C在同一直线上),测得C点的仰角为60°;当叶片OC旋转到最低处OC′时(A、C′、O在同一直线上),测得C′点的仰角为30°.试求风力发电机叶片OC的长度.(结果精确到1米,参考数据: ≈1.414,
≈1.414,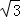 ≈1.732).
≈1.732).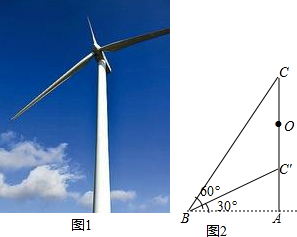
用直尺和圆规作△ABC,使BC=a,AC=b,∠B=35°,若这样的三角形只能作一个,则a,b间满足的关系式是 .
如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
如图是一架人字梯,已知 米, 与地面 的夹角为 ,则两梯脚之间的距离 为
| A. |
米 |
B. |
米 |
C. |
米 |
D. |
米 |
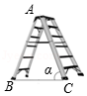
如图,已知点 是以 为直径的半圆上一点, 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,连结 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南,北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线;
(2)如图, 是经过南、北极的圆,地球半径 约为 .弦 ,过点 作 于点 ,连接 .若 ,则以 为半径的圆的周长是北纬 纬线的长度;
(3)参考数据: 取3, , .
小组成员给出了如下解答,请你补充完整:
解:因为 , ,
所以 (填推理依据),
因为 ,所以 ,
在 中, .
(填" "或" " .
所以北纬 的纬线长 .
(填相应的三角形函数值)
(结果取整数).

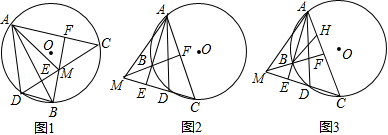
已知 、 是 的两条弦,直线 、 互相垂直,垂足为 ,连接 ,过点 作 ,垂足为 ,直线 交直线 于点 .
(1)如图1,当点 在 内时,连接 , , ,求证: ;
(2)如图2,当点 在 外时,连接 , ,求证: ;
(3)如图3,当点 在 外时, 的平分线与 交于点 ,若 ,求 的值.
如图所示,在平面直角坐标系 中,等腰 的边 与反比例函数 的图象相交于点 ,其中 ,点 在 轴的正半轴上,点 的坐标为 ,过点 作 轴于点 .
(1)已知一次函数的图象过点 , ,求该一次函数的表达式;
(2)若点 是线段 上的一点,满足 ,过点 作 轴于点 ,连结 ,记 的面积为 ,设 ,
①用 表示 (不需要写出 的取值范围);
②当 取最小值时,求 的值.

如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC= .求线段CF的长.
.求线段CF的长.
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求教学楼AB的高度.(参考数据:sin22º≈ ,cos22º≈
,cos22º≈ ,tan22º≈
,tan22º≈ )
)
