初中数学相似三角形的判定与性质解答题

如图，在以线段 $\mathit{AB}$为直径的 $\odot O$上取一点 $C$，连接 $\mathit{AC}$、 $\mathit{BC}$．将 $\mathit{\Delta ABC}$沿 $\mathit{AB}$翻折后得到 $\mathit{\Delta ABD}$．

（1）试说明点 $D$在 $\odot O$上；

（2）在线段 $\mathit{AD}$的延长线上取一点 $E$，使 $A{B}^2=\mathit{AC}·\mathit{AE}$．求证： $\mathit{BE}$为 $\odot O$的切线；

（3）在（2）的条件下，分别延长线段 $\mathit{AE}$、 $\mathit{CB}$相交于点 $F$，若 $\mathit{BC}=2$， $\mathit{AC}=4$，求线段 $\mathit{EF}$的长．

如图，在中，以为直径的交于点，连接，且，连接并延长交的延长线于点，与相切于点．

（1）求证：是的切线；

（2）连接交于点，求证：；

（3）若，求的值．

如图1， $▱\mathit{OABC}$的边 $\mathit{OC}$在 $y$轴的正半轴上， $\mathit{OC}=3$， $A(2,1)$，反比例函数 $y=\frac{k}{x}(x>0)$的图象经过的 $B$．

（1）求点 $B$的坐标和反比例函数的关系式；

（2）如图2，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴的正半轴交于 $M$， $N$两点，若点 $O$和点 $B$关于直线 $\mathit{MN}$成轴对称，求线段 $\mathit{ON}$的长；

（3）如图3，将线段 $\mathit{OA}$延长交 $y=\frac{k}{x}(x>0)$的图象于点 $D$，过 $B$， $D$的直线分别交 $x$轴、 $y$轴于 $E$， $F$两点，请探究线段 $\mathit{ED}$与 $\mathit{BF}$的数量关系，并说明理由．

如图①，半圆O的直径AB＝6，AM和BN是它的两条切线，CP与半圆O相切于点P，并于AM，BN分别相交于C，D两点．

（1）请直接写出∠COD的度数；

（2）求AC•BD的值；

（3）如图②，连接OP并延长交AM于点Q，连接DQ，试判断△PQD能否与△ACO相似？若能相似，请求AC：BD的值；若不能相似，请说明理由．

如图， $\mathit{AB}$是 $\odot O$的直径， $\mathit{PB}$与 $\odot O$相切于点 $B$，连接 $\mathit{PA}$交 $\odot O$于点 $C$，连接 $\mathit{BC}$．

（1）求证： $\angle \mathit{BAC}=\angle \mathit{CBP}$；

（2）求证： $P{B}^2=\mathit{PC}·\mathit{PA}$；

（3）当 $\mathit{AC}=6$， $\mathit{CP}=3$时，求 $\sin \angle \mathit{PAB}$的值．

如图，在正方形 $\mathit{ABCD}$中，点 $E$在 $\mathit{BC}$边上，连接 $\mathit{AE}$， $\angle \mathit{DAE}$的平分线 $\mathit{AG}$与 $\mathit{CD}$边交于点 $G$，与 $\mathit{BC}$的延长线交于点 $F$．设 $\frac{\mathit{CE}}{\mathit{EB}}=\lambda (\lambda >0)$．

（1）若 $\mathit{AB}=2$， $\lambda =1$，求线段 $\mathit{CF}$的长．

（2）连接 $\mathit{EG}$，若 $\mathit{EG}\perp \mathit{AF}$，

①求证：点 $G$为 $\mathit{CD}$边的中点．

②求 $\lambda$的值．

如图，四边形 $\mathit{ABCD}$内接于 $\odot O$， $\mathit{AC}$为 $\odot O$的直径， $D$为 $\stackrel{̂}{\mathit{AC}}$的中点，过点 $D$作 $\mathit{DE}//\mathit{AC}$，交 $\mathit{BC}$的延长线于点 $E$．

（1）判断 $\mathit{DE}$与 $\odot O$的位置关系，并说明理由；

（2）若 $\odot O$的半径为5， $\mathit{AB}=8$，求 $\mathit{CE}$的长．

如图，已知 AD是△ ABC的外角∠ EAC的平分线，交 BC的延长线于点 D，延长 DA交△ ABC的外接圆于点 F，连接 FB， FC．

（1）求证：∠ FBC＝∠ FCB；

（2）已知 FA• FD＝12，若 AB是△ ABC外接圆的直径， FA＝2，求 CD的长．

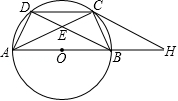
如图，点 A， B， C， D是直径为 AB的⊙ O上的四个点， C是劣弧 $\stackrel{⏜}{\mathit{BD}}$ 的中点， AC与 BD交于点 E．

（1）求证： DC ²＝ CE• AC；

（2）若 AE＝2， EC＝1，求证：△ AOD是正三角形；

（3）在（2）的条件下，过点 C作⊙ O的切线，交 AB的延长线于点 H，求△ ACH的面积．

如图①，在钝角 $\mathit{\Delta ABC}$中， $\angle \mathit{ABC}=30°$， $\mathit{AC}=4$，点 $D$为边 $\mathit{AB}$中点，点 $E$为边 $\mathit{BC}$中点，将 $\mathit{\Delta BDE}$绕点 $B$逆时针方向旋转 $\alpha$度 $(0⩽\alpha ⩽180)$．

（1）如图②，当 $0<\alpha <180$时，连接 $\mathit{AD}$、 $\mathit{CE}$．求证： $\mathit{\Delta BDA}\backsim \mathit{\Delta BEC}$；

（2）如图③，直线 $\mathit{CE}$、 $\mathit{AD}$交于点 $G$．在旋转过程中， $\angle \mathit{AGC}$的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；

（3）将 $\mathit{\Delta BDE}$从图①位置绕点 $B$逆时针方向旋转 $180°$，求点 $G$的运动路程．

如图，一次函数 y＝﹣ $\frac{\sqrt{\text{3}}}{\text{3}}$ x+1的图象与 x轴、 y轴分别交于点 A、 B，以线段 AB为边在第一象限作等边△ ABC．

（1）若点 C在反比例函数 y＝ $\frac{k}{x}$ 的图象上，求该反比例函数的解析式；

（2）点 P（2 $\sqrt{3}$ ， m）在第一象限，过点 P作 x轴的垂线，垂足为 D，当△ PAD与△ OAB相似时， P点是否在（1）中反比例函数图象上？如果在，求出 P点坐标；如果不在，请加以说明．

如图，在矩形 ABCD中， AB＝3， BC＝4，将矩形 ABCD绕点 C按顺时针方向旋转α角，得到矩形 A' B' C' D'， B' C与 AD交于点 E， AD的延长线与 A' D'交于点 F．

（1）如图①，当α＝60°时，连接 DD'，求 DD'和 A' F的长；

（2）如图②，当矩形 A' B' CD'的顶点 A'落在 CD的延长线上时，求 EF的长；

（3）如图③，当 AE＝ EF时，连接 AC， CF，求 AC• CF的值．

如图，在 $\mathit{\Delta ABC}$中，点 $D$， $E$， $F$分别在 $\mathit{AB}$， $\mathit{BC}$， $\mathit{AC}$边上， $\mathit{DE}//\mathit{AC}$， $\mathit{EF}//\mathit{AB}$．

（1）求证： $\mathit{\Delta BDE}\backsim \mathit{\Delta EFC}$．

（2）设 $\frac{\mathit{AF}}{\mathit{FC}}=\frac{1}{2}$，

①若 $\mathit{BC}=12$，求线段 $\mathit{BE}$的长；

②若 $\mathit{\Delta EFC}$的面积是20，求 $\mathit{\Delta ABC}$的面积．

如图， $\mathit{AB}$为 $\odot O$的直径， $C$为 $\odot O$上一点， $D$是弧 $\mathit{BC}$的中点， $\mathit{BC}$与 $\mathit{AD}$、 $\mathit{OD}$分别交于点 $E$、 $F$．

（1）求证： $\mathit{DO}//\mathit{AC}$；

（2）求证： $\mathit{DE}\cdot \mathit{DA}=D{C}^2$；

（3）若 $\tan \angle \mathit{CAD}=\frac{1}{2}$，求 $\sin \angle \mathit{CDA}$的值．

如图， AB是⊙ O的直径，弦 CD与 AB交于点 E，过点 B的切线 BP与 CD的延长线交于点 P，连接 OC， CB．

（1）求证： AE• EB＝ CE• ED；

（2）若⊙ O的半径为3， OE＝2 BE， $\frac{\mathit{CE}}{\mathit{DE}}=\frac{9}{5}$ ，求tan∠ OBC的值及 DP的长．