如图,在边长为 的菱形 中, ,过点 作 于点 ,现将 沿直线 翻折至 的位置, 与 交于点 .则 等于

| A. |
|
B. |
1 |
C. |
|
D. |
|
把边长分别为1和2的两个正方形按如图的方式放置.则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
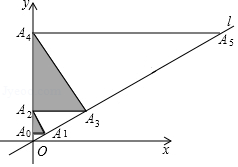
如图,过点 作 轴的垂线交直线 于点 ,过点 作直线 的垂线,交 轴于点 ,过点 作 轴的垂线交直线 于点 , ,这样依次下去,得到△ ,△ ,△ , ,其面积分别记为 , , , ,则 为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在正方形 的对角线 上取一点 .使得 ,连接 并延长 到 ,使 , 与 相交于点 ,若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有

| A. |
①②③ |
B. |
①②③④ |
C. |
①②④ |
D. |
①③④ |
矩形 在平面直角坐标系中的位置如图所示,已知 , ,点 在 轴上,点 在 轴上, 是对角线 上一动点(不与原点重合),连接 ,过点 作 ,交 轴于点 .下列结论:
① ;
②当点 运动到 的中点处时, ;
③在运动过程中, 是一个定值;
④当 为等腰三角形时,点 的坐标为 , .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在矩形 中, 为 中点,以 为边作正方形 ,边 交 于点 ,在边 上取点 使 ,作 交 于点 ,交 于点 ,欧几里得在《几何原本》中利用该图解释了 ,现以点 为圆心, 为半径作圆弧交线段 于点 ,连结 ,记 的面积为 ,图中阴影部分的面积为 .若点 , , 在同一直线上,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中,点 , 分别在 和 上, , 为 边上一点(不与点 , 重合),连接 交 于点 ,则

| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知 是 的直径,点 在 的延长线上, 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,若 的半径为4, ,则 的长为

| A. |
4 |
B. |
|
C. |
3 |
D. |
2.5 |
如图,在正方形 中,连接 ,以点 为圆心,适当长为半径画弧,交 、 于点 , ,分别以 , 为圆心,大于 长的一半为半径画弧,两弧交于点 ,连结 并延长交 于点 ,再分别以 、 为圆心,以大于 长的一半为半径画弧,两弧交于点 , ,作直线 ,分别交 , , 于点 , , ,交 的延长线于点 ,连接 ,下列结论:① ,② ,③ ,④ .其中正确的是

| A. |
①②③ |
B. |
②③④ |
C. |
①③④ |
D. |
①②④ |
如图1,在矩形中,
为
边上一点
,
.将
沿
翻折得到△
,
的延长线交边
于点
,过点
作
交
于点
.
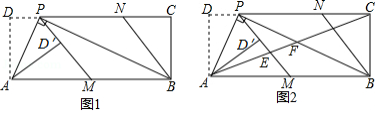
(1)求证:;
(2)请判断四边形的形状,并说明理由;
(3)如图2,连接,分别交
,
于点
,
.若
,求
的值.
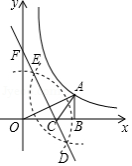
如图,点 在双曲线 上,过点 作 轴,垂足为点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 轴于点 ,交 轴于点 ,连接 .若 ,则 的值为
| A. |
2 |
B. |
|
C. |
|
D. |
|