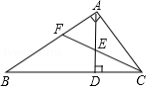
如图,在 中, , , , 的高 与角平分线 交于点 ,则 的值为
| A. |
|
B. |
|
C. |
|
D. |
|
在平面直角坐标系中,,
,
三点的坐标分别为
,
,
,点
在
轴上,点
在直线
上,若
,
于点
,则点
的坐标为 .
在中,
,
.点
是平面内不与点
,
重合的任意一点.连接
,将线段
绕点
逆时针旋转
得到线段
,连接
,
,
.
(1)观察猜想
如图1,当时,
的值是 ,直线
与直线
相交所成的较小角的度数是 .
(2)类比探究
如图2,当时,请写出
的值及直线
与直线
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
当时,若点
,
分别是
,
的中点,点
在直线
上,请直接写出点
,
,
在同一直线上时
的值.
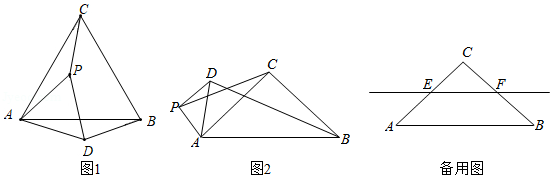
(1)问题发现
如图1,在和
中,
,
,
,连接
,
交于点
.填空:
①的值为 ;
②的度数为 .
(2)类比探究
如图2,在和
中,
,
,连接
交
的延长线于点
.请判断
的值及
的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将绕点
在平面内旋转,
,
所在直线交于点
,若
,
,请直接写出当点
与点
重合时
的长.

如图,在中,
,点
在
上,以线段
的长为半径的
与
相切于点
,分别交
、
于点
、
,连接
并延长,交
的延长线于点
.
(1)求证:.
(2)已知的半径为3.
①若,则
.
②当 时,四边形
为菱形.

如图,在矩形中,点
为
的中点,点
为射线
上一动点,△
与
关于
所在直线对称,连接
,分别交
、
于点
、
,
,
.若
与
相似,则
的长为 .

如图,在中,
,
,
为
的中点,点
为
上一点,若四边形
为正方形(其中点
,
分别在
,
上),则
的面积为 .
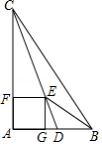
如图,已知 , , ,点 为射线 上一个动点,连接 ,将 沿 折叠,点 落在点 处,过点 作 的垂线,分别交 , 于点 , .当点 为线段 的三等分点时, 的长为 .

如图,在矩形中,
,
,点
为
边上一个动点,连接
,将线段
绕点
顺时针旋转
,点
落在点
处,当点
在矩形
外部时,连接
、
.若
为直角三角形,则
的长 .

如图,小明在笔直的河岸上的点
处,以正对岸明显的标志点
为参照点,设计出两种测量河宽
的方案,绘制了相应的示意图,并用测角仪、卷尺及标杆测得一些数据如下:

(1)请你选择一种方案,结合示意图,简述测量过程;
(2)按照你选定的方案,求河宽.(参考数据:
,
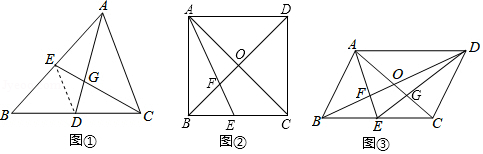
教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在中,
,
分别是边
,
的中点,
,
相交于点
,求证:
证明:连结.
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在中,对角线
、
交于点
,
为边
的中点,
、
交于点
.
(1)如图②,若为正方形,且
,则
的长为 .
(2)如图③,连结交
于点
,若四边形
的面积为
,则
的面积为 .
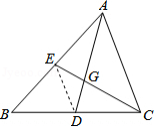
如图,在中,点
在边
上,点
在边
的延长线上,且
,
与
交于点
.
(1)求证:;
(2)若,
,求
的长.
若 的每条边长增加各自的 得△ ,则 的度数与其对应角 的度数相比
| A. |
增加了 |
B. |
减少了 |
| C. |
增加了 |
D. |
没有改变 |