初中数学作图—应用与设计作图试题

如图，在的方格中，的顶点均在格点上．试按要求画出线段，均为格点），各画出一条即可．

如图，在每个小正方形的边长为1的网格中，点，，均在格点上．

（1）的长等于　　；

（2）在的内部有一点，满足，请在如图所示的网格中，用无刻度的直尺，画出点，并简要说明点的位置是如何找到的（不要求证明）　　．

如图，在每个小正方形的边长为1的网格中， $A$ ， $E$ 为格点， $B$ ， $F$ 为小正方形边的中点， $C$ 为 $\mathit{AE}$ ， $\mathit{BF}$ 的延长线的交点．

（Ⅰ） $\mathit{AE}$ 的长等于 　　；

（Ⅱ）若点 $P$ 在线段 $\mathit{AC}$ 上，点 $Q$ 在线段 $\mathit{BC}$ 上，且满足 $\mathit{AP}=\mathit{PQ}=\mathit{QB}$ ，请在如图所示的网格中，用无刻度的直尺，画出线段 $\mathit{PQ}$ ，并简要说明点 $P$ ， $Q$ 的位置是如何找到的（不要求证明） 　　．

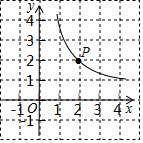
如图，反比例函数的图象过格点（网格线的交点）．

（1）求反比例函数的解析式；

（2）在图中用直尺和铅笔画出两个矩形（不写画法），要求每个矩形均需满足下列两个条件：

①四个顶点均在格点上，且其中两个顶点分别是点，点；

②矩形的面积等于的值．

图①，图②均为的正方形网格，每个小正方形的顶点称为格点．在图①中已画出线段，在图②中已画出线段，其中、、、均为格点，按下列要求画图：

（1）在图①中，以为对角线画一个菱形，且，为格点；

（2）在图②中，以为对角线画一个对边不相等的四边形，且，为格点，．

图①、图②、图③均是的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点、、、、、均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．

（1）在图①中以线段为边画一个，使其面积为6．

（2）在图②中以线段为边画一个，使其面积为6．

（3）在图③中以线段为边画一个四边形，使其面积为9，且．

图①、图②、图③都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点．线段的端点在格点上．

（1）在图①、图2中，以为边各画一个等腰三角形，且第三个顶点在格点上；（所画图形不全等）

（2）在图③中，以为边画一个平行四边形，且另外两个顶点在格点上．

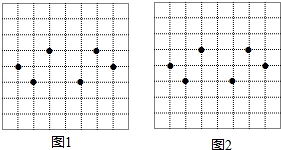
图1，图2都是的正方形网格，每个小正方形的顶点成为格点，每个小正方形的边长均为1，在每个正方形网格中标注了6个格点，这6个格点简称为标注点

（1）请在图1，图2中，以4个标注点为顶点，各画一个平行四边形（两个平行四边形不全等）；

（2）图1中所画的平行四边形的面积为　　．

如图，六个完全相同的小长方形拼成了一个大长方形， $\mathit{AB}$ 是其中一个小长方形的对角线，请在大长方形中完成下列画图，要求：①仅用无刻度直尺，②保留必要的画图痕迹．

（1）在图1中画出一个 $45°$ 角，使点 $A$ 或点 $B$ 是这个角的顶点，且 $\mathit{AB}$ 为这个角的一边；

（2）在图2中画出线段 $\mathit{AB}$ 的垂直平分线．

根据下列条件画图，如图示点A、B、C分别代表三个村庄：

（1）画射线AC，画线段AB
（2）若线段AB是连结A村和B村的一条公路，现C村庄也要修一条公路与A、B两村庄之间的公路连通，为了减少修路开支，C村庄应该如何修路？请在同一图上用三角板画出示意图，并说明画图理由．

如图是由边长都是1的小正方形组成的网格．请以图中线段BC为边，作△PBC，使P在格点上，并满足：

（1）图甲中的△PBC是直角三角形，且面积是△ABC面积2倍；
（2）图乙中的△PBC是等腰非直角三角形．