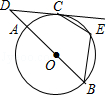
如图, 为 的切线, 为切点,若 , 、 为圆周上两点,且 ,则 等于

A. B. C. D.
如图,已知 为半圆 的直径, 为半圆 上一点,连接 , ,过点 作 于点 ,过点 作半圆 的切线交 的延长线于点 ,连接 并延长交 于点 .
(1)求证: ;
(2)若半圆 的直径为10, ,求 的长.

如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若 ,则∠D的度数为 .

如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若 ,则∠DBA的大小是( )

A.15°B.30°C.60°D.75°
如图, AB为⊙ O的直径,直线 l与⊙ O相切于点 C, ,垂足为 D, AD交⊙ O于点 E,连接 OC、 BE.若 , ,则线段 DC的长为 .
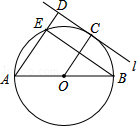
如图,若以平行四边形一边 AB为直径的圆恰好与对边 CD相切于点 D,则∠ C= 度.

如图,在矩形 ABCD中, AB=5, BC=10 ,一圆弧过点 B和点 C,且与 AD相切,则图中阴影部分面积为 .

如图,CD是⊙O的弦,AB是直径,且 ,连接AC、AD、OD,其中 ,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据: , ).

如图,在Rt△ABC中, ,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
(1)求证:AD平分∠CAB;
(2)若 于点H,FH平分 .
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.

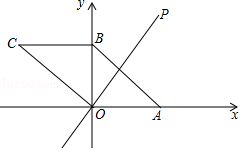
如图,在平面直角坐标系xOy中,▱ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线 上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与▱ABCO的边相切时,P点的坐标为 .
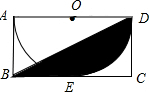
如图,矩形 ABCD中, BC=4, CD=2,以 AD为直径的半圆 O与 BC相切于点 E,连接 BD,则阴影部分的面积为 .(结果保留π)
如图,一把直尺,60°的直角三角板和光盘如图摆放, A为60°角与直尺交点, AB=3,则光盘的直径是( )

| A. |
3 |
B. |
|
C. |
6 |
D. |
|
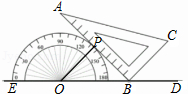
以 O为中心点的量角器与直角三角板 ABC如图摆放,直角顶点 B在零刻度线所在直线 DE上,且量角器与三角板只有一个公共点 P,则∠ CBD的度数是( )
| A. |
45°10' |
B. |
44°50' |
C. |
46°10' |
D. |
不能确定 |
如图, AB是⊙ O的直径,点 C在⊙ O上,过点 C的切线与 BA的延长线交于点 D,点 E在 上(不与点 B, C重合),连接 BE, CE.若∠ D=40°,则∠ BEC= 度.