(8分)如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF. 求证:(1)△ABE≌△CDF;(2)AE∥CF.
求证:(1)△ABE≌△CDF;(2)AE∥CF.
如图,等腰梯形ABCD中,AB//CD,AD=BC,CE⊥AB于E,AE=DE,AF⊥DE于F,请你判断线段AF与图中的哪条线段相等,先写出你的猜想,再说明理由.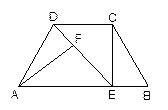
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,问出发多少秒钟时△DPQ的面积等于31cm2?
如图1,在 中,
中, 为锐角,点
为锐角,点 为射线
为射线 上一点,联结
上一点,联结 ,以
,以 为一边且在
为一边且在 的右侧作正方形
的右侧作正方形 .
.
(1)如果 ,
, ,
,
①当点 在线段
在线段 上时(与点
上时(与点 不重合),如图2,线段
不重合),如图2,线段 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段 的数量关系为 ;
的数量关系为 ;
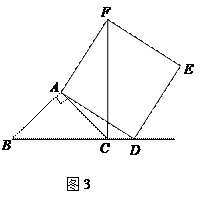
②当点 在线段
在线段 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
 |
|||||
 |
|||||
 |
|||||
(2)如果 ,
,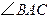 是锐角,点
是锐角,点 在线段
在线段 上,当
上,当 满足什么条件时,
满足什么条件时, (点
(点 不重合),并说明理由.
不重合),并说明理由.
如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM BE,垂足为M,AM交BD于点F.
BE,垂足为M,AM交BD于点F.
(1)求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

(本题8分)利用一面长45米的墙,用80m长的篱笆围成一个矩形场地。
⑴怎样才能使矩形场地面积为750㎡?
⑵能否使所围矩形场地的面积为810㎡,为什么?
如图, F、C是线段AD上的两点,AB∥DE,BC∥EF ,AF=DC,
,AF=DC,
连结AE、BD,求证:四 边形ABDE是平行四边形。
边形ABDE是平行四边形。
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE。已知∠BAC=30º,EF⊥AB,垂足为F,连结DF。
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形。
(8分)如图,将直角三角形纸片ABC沿边BC所在直线向右平移,使B点移至斜
边BC的中点E处,连接AD、AE、CD。
(1)求证:四边形AECD是菱形。
(2)若直角三角形纸片ABC的斜边BC的长为100cm,且AC=60cm.求ED的长 和四边形AECD的面积;
如图,在梯形ABCD中,AD∥BC,AC、BD是对角线.过点D作DE
∥AC,交BC的延长线于点E.
(1)判断四边形ACED的形 状并证明;
状并证明;
(2)若AC=D B,求证:梯形ABCD是等腰梯形.
B,求证:梯形ABCD是等腰梯形.