如图：在四边形ABCD中，E是AB上的一点，△ADE和△BCE都是等边三角形，点P、Q、M、N分别为AB、BC、CD、DA的中点，四边形MNPQ什么形状？说明理由。
(本题12分)如图甲，在△ABC中，E是AC边上的一点，
(1)在图甲中，作出以BE为对角线的平行四边形BDEF，使D、F分别在BC和AB边上；
(2)改变点E的位置，则图甲中所作的平行四边形BDEF有没有可能为菱形？若有，请在图乙中作出点E的位置（用尺规作图，并保留作图痕迹）；若没有，请说明理由．
 |
(本题8分)如图，△ABC中，已知BE⊥AD，CF⊥AD，且BE＝CF．
（1）请你判断AD是△ABC的中线还是角平分线？请证明你的结论．
（2）连接BF、CE，若四边形BFCE是菱形，则△ABC中应添加一个条件 。
（填上你认为正确的一个条件即可）
如图，矩形ABCD中，对角线AC、BD交于点O，DE∥OC，CE∥OD，试判断四边形OCDE是何特殊四边形，并加以证明。（8′）
如图，在平行四边形ABCD中，对角线AC、BD相交于点O，AF⊥BD，CE⊥BD，垂足分别为E、F；
（1）连结AE、CF，得四边形AFCE，试判断四边形AFCE是下列图形中的哪一种？
①平行四边形；②菱形；③矩形；
（2）请证明你的结论；
阅读材料并解答问题
如图①，以Rt△ABC的直角边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连结EG，可以得出结论△ABC的面积与△AEG的面积相等.
(1)在图①中的△ABC的直角边AB上任取一点H，连结CH，以BH、HC为边分别向外作正方形HBDE和正方形HCFG，连结EG，得到图②，则△HBC的面积与△HEG的面积的大小关系为 .
(2)如图③，若图形总面积是a，其中五个正方形的面积和是b，则图中阴影部分的面积是 .
(3)如图④，点A、B、C、D、E都在同一直线上，四边形X、Y、Z都是正方形，若图形总面积是m，正方形Y的面积是n，则图中阴影部分的面积是 .
图① 图② 图③ 图④
（每小题5分，共10分）如图，在Rt△ABC中，∠ABC=90°将Rt△ABC绕点C顺时针方向旋转60°得到△DEC点E在AC上，再将Rt△ABC沿着AB所在直线翻转180°得到△ABF连接AD.
（1）求证：四边形AFCD是菱形；
（2）连接BE并延长交AD于G连接CG，请问：
四边形ABCG是什么特殊平行四边形？为什么？
（每小题5分，共10分）已知，如图，四边形ABCD中∠B=90°，AB=9，BC=12，AD=8，CD=17
试求：（1）AC的长； （2）四边形ABCD的面积；
已知矩形ABCD，现将矩形沿对角线BD折叠，得到如图所示的图形，
（1）求证：△ABE≌△C’ DE
（2）若AB＝6，AD＝10，求S△ABE
（本题10分）如图，梯形ABCD中，AD∥BC，BC=2AD，F、G分别为边BC、CD的中点，连接AF，FG，过D作DE∥GF交AF于点E。
（1）证明△AED≌△CGF
（2）若梯形ABCD为直角梯形，判断四边形DEFG是什么特殊四边形？并证明你的结论。
 |
如图，在平行四边形ABCD中，
为
上两点，且
，
．
(1).求证：
；
(2).四边形
是矩形．
(本题满分10分)
如图，一艘轮船由A港沿北偏东
方向航行10km至B港，再沿北偏西
方向航行10km到达C港.
（1）求A、C两港之间的距离（精确到1km）
（2）求点C相对于点A位置.
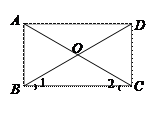
(10分)如图，四边形ABCD是平行四边形，AC、BD交于点O，∠1＝∠2．
(1)求证：四边形ABCD是矩形；
(2)若∠BOC＝120°，AB＝4cm，求四边形ABCD的面积．
 |
矩形ABCD中，点E在边AD上，EF⊥CE且与AB相交于点F，若DE=2，AD+DC=8，且CE=EF，求AE的长。
粤公网安备 44130202000953号