初中数学圆填空题

《九章算术》被尊为古代数学“群经之首”，其卷九勾股篇记载：今有圆材埋于壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？如图，大意是，今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深 $\mathit{CD}$等于1寸，锯道 $\mathit{AB}$长1尺，问圆形木材的直径是多少？ $(1$尺 $=10$寸）

答：圆材直径 　　寸．

边长为 $4\mathit{cm}$的正六边形，它的外接圆与内切圆半径的比值是 　　．

一条弧所对的圆心角为 $135°$，弧长等于半径为 $5\mathit{cm}$的圆的周长的3倍，则这条弧的半径为 　　 $\mathit{cm}$．

如图，在 $\text{Rt}\Delta \text{AOB}$中， $\angle \mathit{AOB}=90°$， $\mathit{OA}=4$， $\mathit{OB}=6$，以点 $O$为圆心，3为半径的 $\odot O$，与 $\mathit{OB}$交于点 $C$，过点 $C$作 $\mathit{CD}\perp \mathit{OB}$交 $\mathit{AB}$于点 $D$，点 $P$是边 $\mathit{OA}$上的动点，则 $\mathit{PC}+\mathit{PD}$的最小值为 　　．

若一个圆锥的底面半径为 $1\mathit{cm}$，它的侧面展开图的圆心角为 $90°$，则这个圆锥的母线长为 　　 $\mathit{cm}$．

如图，在 $\odot O$中， $\mathit{AB}$是直径，弦 $\mathit{AC}$的长为 $5\mathit{cm}$，点 $D$在圆上且 $\angle \mathit{ADC}=30°$，则 $\odot O$的半径为 　　 $\mathit{cm}$．

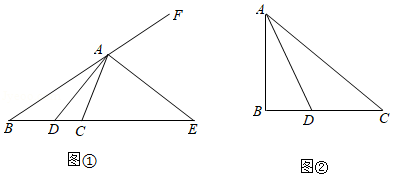
已知，如图①，若 $\mathit{AD}$是 $\mathit{\Delta ABC}$中 $\angle \mathit{BAC}$的内角平分线，通过证明可得 $\frac{\mathit{AB}}{\mathit{AC}}=\frac{\mathit{BD}}{\mathit{CD}}$，同理，若 $\mathit{AE}$是 $\mathit{\Delta ABC}$中 $\angle \mathit{BAC}$的外角平分线，通过探究也有类似的性质．请你根据上述信息，求解如下问题：

如图②，在 $\mathit{\Delta ABC}$中， $\mathit{BD}=2$， $\mathit{CD}=3$， $\mathit{AD}$是 $\mathit{\Delta ABC}$的内角平分线，则 $\mathit{\Delta ABC}$的 $\mathit{BC}$边上的中线长 $l$的取值范围是 　　．

如图，作 $\odot O$的任意一条直径 $\mathit{FC}$，分别以 $F$、 $C$为圆心，以 $\mathit{FO}$的长为半径作弧，与 $\odot O$相交于点 $E$、 $A$和 $D$、 $B$，顺次连接 $\mathit{AB}$、 $\mathit{BC}$、 $\mathit{CD}$、 $\mathit{DE}$、 $\mathit{EF}$、 $\mathit{FA}$，得到六边形 $\mathit{ABCDEF}$，则 $\odot O$的面积与阴影区域的面积的比值为 　　．

一个圆柱形橡皮泥，底面积是 $12c{m}^2$．高是 $5\mathit{cm}$．如果这个橡皮泥的一半，把它捏成高为 $5\mathit{cm}$的圆锥，则这个圆锥的底面积是 　　 $c{m}^2$．

如图所示的网格中，每个小正方形的边长均为1，点 $A$， $B$， $D$均在小正方形的顶点上，且点 $B$， $C$在 $\stackrel{̂}{\mathit{AD}}$上， $\angle \mathit{BAC}=22.5°$，则 $\stackrel{̂}{\mathit{BC}}$的长为 　　．

如图，要用一个扇形纸片围成一个无底盖的圆锥（接缝处忽略不计），若该圆锥的底面圆周长为 $20\mathit{\pi cm}$，侧面积为 $240\mathit{\pi c}{m}^2$，则这个扇形的圆心角的度数是 　　度．

小明很喜欢专研问题，一次数学杨老师拿来一个残缺的圆形瓦片（如图所示）让小明求瓦片所在圆的半径，小明连接瓦片弧线两端AB，量的弧AB的中心C到AB的距离 $\mathit{CD}＝1.6\mathit{cm}$， $\mathit{AB}＝6.4\mathit{cm}$，很快求得圆形瓦片所在圆的半径为 　　cm．

如图．在边长为6的正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{BC}=3\mathit{BE}$且 $\mathit{BE}=\mathit{CF}$， $\mathit{AE}\perp \mathit{BF}$，垂足为 $G$， $O$是对角线 $\mathit{BD}$的中点，连接 $\mathit{OG}$、则 $\mathit{OG}$的长为 　　．

如图，圆锥的高是4，它的侧面展开图是圆心角为 $120°$的扇形，则圆锥的侧面积是 　　（结果保留 $\pi )$．

在 $\mathit{\Delta ABC}$中， $\angle \mathit{ABC}=90°$， $\mathit{AB}=2$， $\mathit{BC}=3$．点 $D$为平面上一个动点， $\angle \mathit{ADB}=45°$，则线段 $\mathit{CD}$长度的最小值为 　　．