初中数学圆填空题

（本小题9分）如图、在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。

（1）求证：CE=CF
(2)在图1中，若G在AD上，且∠GCE=45°,则GE=BE+GD成立吗？为什么？
（3）运用（1）（2）解答中积累的经验和知识，完成下题：
如图2，四边形ABCD中，AD∥BC(BC＞AD),∠B=90°,AB=BC=12,E是AB上一点，
且∠DCE=45°，BE=4，求DE的 长。

红丝带是关注艾滋病防治问题的国际性标志.将宽为的红丝带交叉成60°角重叠在一起（如图），则重叠四边形的面积为_______

如图1，小正方形ABCD的面积为1，把它的各边延长一倍得到新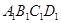正方形，正方形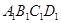的面积为           ；再把正方形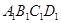的各边延长一倍得到正方形（如图2），如此进行下去，正方形的面积为            ．（用含有n的式子表示，n为正整数）

已知等腰梯形的面积为24cm²，中位线长为6cm，则等腰梯形的高为_________cm．

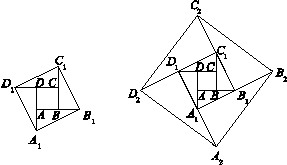
如图，平行四边形ABCD中，AD＝5cm，AB⊥BD，点O是两条对角线的交点，OD＝2，则AB＝     ▲    cm．

如图，在梯形ABCD中，AD∥BC，点E、F、G、H是两腰上的点，AE=EF=FB，CG=GH=HD，且四边形EFGH的面积为6cm²，则梯形ABCD的面积为  ▲ cm²．

如图，在菱形ABCD中，对角线AC，BD分别等于8和6，将BD沿CB的方向平移，使D与A重合，B与CB延长线上的点E重合，则四边形AECD的面积等于   ▲   ．

如图，直线上有三个正方形，若的面积分别为6和12，则的面积为_________.

如图，EF过矩形ABCD对角线的交点O，且分别交AB、CD于E、F，那么阴影部分的面积是矩形ABCD的面积的________.

如图，□ABCD的周长是16，则AB+AD=        .

已知ｍ是方程ｘ²－ｘ－１＝０的一个根，则代数 ｍ²－ｍ＝　　　　　　         

已知线段AB和线段CD分别为一个梯形的两个底边，且BC⊥CD，AB=2√3，BC=3，S△BCD=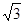，则AD等于           。

某体育馆用大小相同的长方形木块镶嵌地面，第一次铺2块，如图（1）；第二次把第一次铺的完全围起来，如图（2），第三次把第二次铺的完全围起来，如图（3）；……以此方法，第n次铺完后，用字母n表示第几次镶嵌所使用的木块数为           。

如图所示，四边形ABCD是一个梯形，AB∥CD，∠ABC=90^。，AB="9" cm，BC="8" cm，CD="7" cm，M是AD的中点，过M做AD的垂线交BC于N，则BN的长等于           。

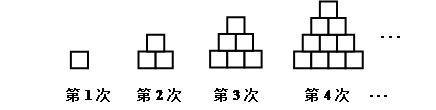
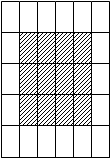
用边长为1cm的小正方形搭如下的塔状图形，则第n次所搭图形的周长是_    cm（用含n的代数式表示）．