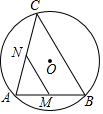
如图, 是 的弦, ,点 是 上的一个动点,且 ,若点 、 分别是 、 的中点,则 长的最大值是 .
如图是一个几何体的三视图(图中尺寸单位: ,根据图中所示数据计算这个几何体的表面积是 .

如图, , , , 为 上一点, ,以 为圆心,以
为半径的圆与 相切于点 ,与 相交于点 ,连接 、 ,则图中阴影部分的面积是 .

用一块圆心角为 的扇形铁皮,做一个高为 的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是 .
如图,正方形 的边长为 , 为 边的中点, 、 的圆心分别在边 、 上,这两段圆弧在正方形内交于点 ,则 、 间的距离为 .

如图,在 中, 为 的直径, 与 相切于点 ,与 相交于点 ,已知 , ,则 的长为 .

如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形 .已知 ,取 的中点 ,过点 作 交 于点 ,点 是 上一点.若将扇形 沿 翻折,点 恰好与点 重合,用剪刀沿着线段 , , 依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 .

阅读理解:如图1, 与直线 、 都相切,不论 如何转动,直线 、 之间的距离始终保持不变(等于 的直径),我们把具有这一特性的图形称为“等宽曲线”,图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进,据说,古埃及人就是利用这样的方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”,如图4,夹在平行线 , 之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变,若直线 , 之间的距离等于 ,则莱洛三角形的周长为 .

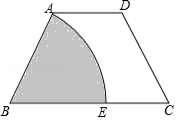
如图,四边形 中, , ,以点 为圆心, 为半径的圆弧与 交于点 ,四边形 是平行四边形, ,则扇形(图中阴影部分)的面积是 .