初中数学圆填空题

已知四边形ABCD是正方形，等腰直角△AEF的直角顶点E在直线BC上（不与点B，C重合），FM⊥AD，交射线AD于点M．

（1）当点E在边BC上，点M在边AD的延长线上时，如图①，求证：AB+BE=AM；
（提示：延长MF，交边BC的延长线于点H．）
（2）当点E在边CB的延长线上，点M在边AD上时，如图②；当点E在边BC的延长线上，点M在边AD上时，如图③．请分别写出线段AB，BE，AM之间的数量关系，不需要证明；
（3）在（1），（2）的条件下，若BE=，∠AFM=15°，则AM=     ．

如图，平行四边形ABCD的对角线AC、BD相交于点O，BC=9，AC=8，BD=14，则△AOD的周长为       ．

如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA=OB=a，以线段AB为边在第一象限作正方形ABCD，CD的延长线交x轴于点E，再以CE为边作第二个正方形ECGF，…，依此方法作下去，则第n个正方形的边长是         ．

如图，在Rt△ABC中，∠ACB=90°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF=BC．若AB=10，则EF的长是          ．

如图，E的矩形ABCD中BC边的中点，将△ABE沿AE折叠到△AEF，F在矩形ABCD内部，延长AF交DC于G点．若∠AEB=55°，求∠DAF=           °．

某花木场有一块如等腰梯形ABCD的空地（如图），各边的中点分别是E、F、G、H，用篱笆围成的四边形EFGH场地的周长为40cm，则对角线AC＝             cm．

在平行四边形ABCD中，BC边上的高为4，AB=5，AC=2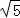，则平行四边形ABCD的周长等于             ．

如图，矩形ABCO中，OA在x轴上，OC在y轴上，且OA=2，AB=5，把△ABC沿着AC对折得到△AB′C，AB′交y轴于D点，则D点的坐标为                 ．

如图，在正方形ABCD外作等腰直角△CDE，DE=CE，连接AE，则sin∠AED=        ．

在3×3的方格中，A、B、C、D、E、F分别位于如图所示的小正方形的顶点上，从C、D、E、F四点中任意取一点，以所取得一点及点A、B为顶点画三角形，则所画三角形为等腰三角形的概率是            ．

正方形A₁B₁C₁O，A₂B₂C₂C₁，A₃B₃C₃C₂，…按如图的方式放置．点A₁，A₂，A₃，…和点C₁，C₂，C₃，…分别在直线y=x+1和x轴上，则点B₆的坐标是            ．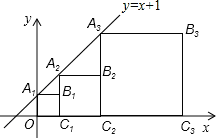

如图，分别以直角三角形的三边向外作正方形，则正方形B的面积为             ．

如图，正方形ABCD的边长为，E，F分别是AB，BC的中点，AF与DE，DB分别交于点M，N，则△DMN的面积=        ．

如图，在菱形ABCD中，∠ABC=60°，BC=1cm，以DC为边在菱形的外部作正三角形CDE，连接AE，则AE=       cm．

如图，□ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=4，则CD的长为      ．