如图, 中, ,以点 为圆心, 为半径作 , 为 上一点,连接 、 , , 平分 .
(1)求证: 是 的切线;
(2)延长 、 相交于点 ,若 ,求 的值.
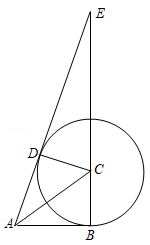
如图所示, 是 的直径,点 、 是 上不同的两点,直线 交线段 于点 、交过点 的直线 于点 ,若 ,且 .
(1)求证:直线 是 的切线;
(2)连接 、 、 、 ,若 .
①求证: ;
②过点 作 ,交线段 于点 ,点 为线段 的中点,若 ,求线段 的长度.

将一物体(视为边长为 米的正方形 从地面 上挪到货车车厢内.如图所示,刚开始点 与斜面 上的点 重合,先将该物体绕点 (E)按逆时针方向旋转至正方形 的位置,再将其沿 方向平移至正方形 的位置(此时点 与点 重合),最后将物体移到车厢平台面 上.已知 , ,过点 作 于点 , 米, 米.
(1)求线段 的长度;
(2)求在此过程中点 运动至点 所经过的路程.

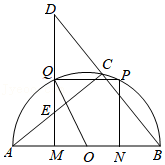
如图,点 为以 为直径的半圆的圆心,点 , 在直径 上,点 , 在 上,四边形 为正方形,点 在 上运动(点 与点 , 不重合),连接 并延长交 的延长线于点 ,连接 交 于点 ,连接 .
(1)求 的值;
(2)求 的值;
(3)令 , ,直径 , 是常数),求 关于 的函数解析式,并指明自变量 的取值范围.
如图,在 中, , ,以点 为圆心, 为半径的圆交 的延长线于点 ,过点 作 的平行线,交 于点 ,连接 .
(1)求证: 为 的切线;
(2)若 ,求弧 的长.

如图1, 是 的直径,点 是 上一动点,且不与 , 两点重合, 的平分线交 于点 ,过点 作 ,交 的延长线于点 .

(1)求证: 是 的切线;
(2)求证: ;
(3)如图2,原有条件不变,连接 , ,延长 至点 , 的平分线交 的延长线于点 , 的平分线交 的平分线于点 .求证:无论点 如何运动,总有 .
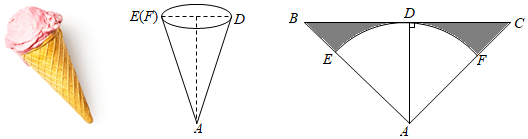
某种冰激凌的外包装可以视为圆锥,它的底面圆直径 与母线 长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中 , .将扇形 围成圆锥时, , 恰好重合.
(1)求这种加工材料的顶角 的大小.
(2)若圆锥底面圆的直径 为 ,求加工材料剩余部分(图中阴影部分)的面积.(结果保留
如图,点 在以 为直径的 上, 的角平分线与 相交于点 ,与 相交于点 ,延长 至 ,连结 ,使得 ,过点 作 的平行线与 的延长线交于点 .
(1)求证: 与 相切;
(2)试给出 、 、 之间的数量关系,并予以证明.

如图,在半径为 的 中, 是 的直径, 是过 上一点 的直线,且 于点 , 平分 , 是 的中点, .
(1)求证: 是 的切线;
(2)求 的长.

如图, 是 的直径, 为 上一点, 为 的中点,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

如图,在 中, ,以 的中点 为圆心, 为直径的圆交 于 , 是 的中点, 交 的延长线于 .
(1)求证: 是圆 的切线:
(2)若 , ,求 的长.

如图,在菱形 中, 是对角线 上一点 , ,垂足为 ,以 为半径的 分别交 于点 ,交 的延长线于点 , 与 交于点 .
(1)求证: 是 的切线;
(2)若 是 的中点, , .
①求 的长;
②求 的长.
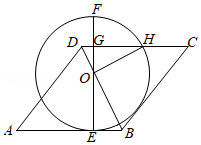
如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分面积.

如图, 是 的直径, , 是 上两点, 是 的中点,过点 作 的垂线,垂足是 .连接 交 于点 .
(1)求证: 是 的切线;
(2)若 ,求 的值.

等面积法是一种常用的、重要的数学解题方法.它是利用“同一个图形的面积相等”、“分割图形后各部分的面积之和等于原图形的面积”、“同底等高或等底同高的两个三角形面积相等”等性质解决有关数学问题,在解题中,灵活运用等面积法解决相关问题,可以使解题思路清晰,解题过程简便快捷.
(1)在直角三角形中,两直角边长分别为3和4,则该直角三角形斜边上的高的长为 ,其内切圆的半径长为 ;
(2)①如图1, 是边长为 的正 内任意一点,点 为 的中心,设点 到 各边距离分别为 , , ,连接 , , ,由等面积法,易知 ,可得 ;(结果用含 的式子表示)

②如图2, 是边长为 的正五边形 内任意一点,设点 到五边形 各边距离分别为 , , , , ,参照①的探索过程,试用含 的式子表示 的值.(参考数据: ,
(3)①如图3,已知 的半径为2,点 为 外一点, , 切 于点 ,弦 ,连接 ,则图中阴影部分的面积为 ;(结果保留
②如图4,现有六边形花坛 ,由于修路等原因需将花坛进行改造,若要将花坛形状改造成五边形 ,其中点 在 的延长线上,且要保证改造前后花坛的面积不变,试确定点 的位置,并说明理由.
