如图1,在直角梯形ABCD中,AD∥BC,∠B=∠A=90°,AD=a,BC=b,AB=c,
操作示例:
我们可以取直角梯形ABCD的非直角腰CD的中点P,过点P作PE∥AB,裁掉△PEC,并将△PEC绕点P逆时针旋转180°拼接到△PFD的位置,构成新的图形(如图2).
思考发现:
判断图2中四边形ABEF的形状: ;四边形ABEF的面积是 。(用含字母的代数式表示)
实践探 究:
究:
类比图2的剪拼方法,请你就图3(已知:AB∥DC)画出剪拼成一个平行四边形的示意图.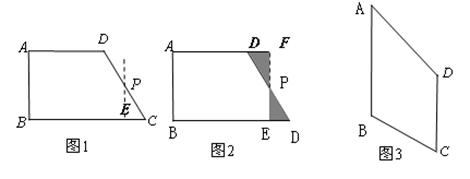
联想拓展:
小明通过探究后发 现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
现:在一个四边形中,只要有一组对边平行,就可以剪拼成平行四边形.
如图4,在梯形ABCD中,AD∥BC,E是CD的中点, EF⊥AB于点F,AB=5,EF=4,求梯形ABCD的面积。
如图5的多边形中,AE=CD,AE∥CD,能否象上面剪切方法一样沿一条直线进行剪切,拼成一平行四边形?若能,请你在图中画出剪拼的示意图并作必要的文字说明;若不能,简要说明理由.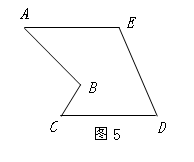
如图,正方形ABCD的边长是2,M是AD的中点.点E从点A出发,沿AB运动到点B停止.连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连接EG、FG.
(1)设AE=x时,△EGF面积为y.求y关于x的函数关系式,并填写自变量x的取值范围;
(2)P是MG的中点,请直接写出点P运动路线的长.
如图,四边形ABCD的对角线AC、BD相交于点O,△ABC≌△BAD.求证:(1)OA=OB;(2)AB∥CD.
如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若 ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少?
(本题满分8分)
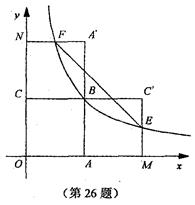
如图,四边形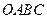 是面积为4的正方形,函数
是面积为4的正方形,函数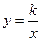 (
( )的图象经过点
)的图象经过点 .
.
(1)求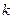 的值;
的值;
(2)将正方形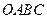 分别沿直线
分别沿直线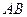 、
、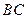 翻折,得到正方形
翻折,得到正方形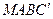 、
、 .设线段
.设线段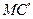 、
、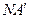 分别与函数
分别与函数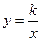 (
( )的图象交于点
)的图象交于点 、
、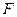 ,求线段EF所在直线的解析式.
,求线段EF所在直线的解析式.
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连结EF,试判断四边形BCEF的形状,并说明理由.
如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的一条面积等分线.如:平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线.
(1)三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有___;
(2)如图1,梯形ABCD中,AB∥DC,如果延长DC到E,使CE=AB,连接AE,那么有S梯形ABCD=S△ADE.请你给出这个结论成立的理由,并过点A作出梯形ABCD的面积等分线(不写作法,保留作图痕迹);
(3)如图,四边形ABCD中,AB与CD不平行,S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并给出证明;若不能,说明理由.
如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC= .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
某公园有一滑梯,横截面如图薪示,AB表示楼梯,BC表示平台,CD表示滑道.若点E,F均在线段AD上,四边形BCEF是矩形,且sin∠BAF= ,BF=3米,BC=1米,CD=6米.求:
,BF=3米,BC=1米,CD=6米.求:
(1) ∠D的度数;
(2)线段AE的长.
(本小题满分10分)
如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ。设AP=x。
(1)当PQ∥AD时,求x的值;
(2)当线段PQ的垂直平分线与BC边相交时,求x的取值范围;
(3)当线段PQ的垂直平分线与BC边相交时,设交点为E,连接EP、EQ,设△EPQ的面积为S,求S关于x的函数关系式,并写出S的取值范围。
(本小题满分7分)
如图,在△ABC中,AB=AC,D为BC中点。四边形ABDE是平行四边形。
求证:四边形ADCE是矩形
如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE.
(1)求证:∠DAE=∠DCE;
(2)当AE=2EF时,判断FG与EF有何等量关系?并证明你的结论?
如下图,6个一样大的小正方形纸片,现要把它们粘贴在一起,拼成一个正方体的平面展开图,然后折成一个正方体.
| |
|
|
|
|
|
|
|
|
|
|
(1) 你认为应该怎样粘贴才是正方体的平面展开图?请在下面方格纸中画你的图.(要求画一个即可)
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
(2)在你所画的一个平面展开图中,把1、2、3、4、5、6这六个数分别填入六个正方形中,使得翻折成正方体后,相对的两个面上的数字的和都相等.
如图,在□ABCD中,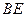 平分
平分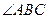 交
交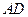 于点
于点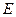 ,
,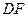 平分
平分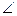
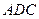 交
交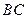 于点
于点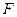 .
.
求证:(1)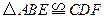 ;
;
(2)若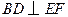 ,则判断四边形
,则判断四边形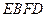 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.
用同样规格的黑白两种颜色的正方形,按如图的方式拼图,请根据图中的信息完成下列的问题.
(1)在图②中用了 块黑色正方形,在图③中用了 块黑色正方形;
(2)按如图的规律继续铺下去,那么第 个图形要用 块黑色正方形;
个图形要用 块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完90块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.