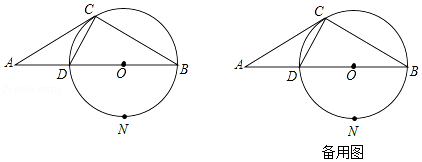
如图1, 为 上一点,点 在直径 的延长线上,且 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , ,求 的半径;
(3)如图2,在(2)的条件下, 的平分线 交 于点 ,交 于点 ,连结 .求 的值.

如图,在 中, 是直径, 是弦, ,垂足为 ,过点 的 的切线与 延长线交于点 ,连接 .
(1)求证: 为 的切线;
(2)若 半径为3, ,求 .

如图, 的半径为1,点 是 的直径 延长线上的一点, 为 上的一点, , .
(1)求证:直线 是 的切线;
(2)求 的面积;
(3)点 在 上运动(不与 、 重合),过点 作 的垂线,与 的延长线交于点 .
①当点 运动到与点 关于直径 对称时,求 的长;
②当点 运动到什么位置时, 取到最大值,并求出此时 的长.
已知平面直角坐标系中,点 , 和直线 (其中 , 不全为 ,则点 到直线 的距离 可用公式 来计算.
例如:求点 到直线 的距离,因为直线 可化为 ,其中 , , ,所以点 到直线 的距离为: .
根据以上材料,解答下列问题:
(1)求点 到直线 的距离;
(2)在(1)的条件下, 的半径 ,判断 与直线 的位置关系,若相交,设其弦长为 ,求 的值;若不相交,说明理由.
如图, , 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 , 分别是 , 的中点, 所在直线交 于点 , , ,求 的长.
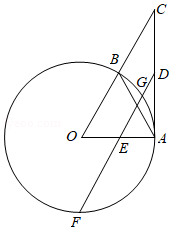
如图, 是 的内接三角形,过点 作 的切线交 的延长线于点 , 是 的直径,连接 .
(1)求证: ;
(2)若 , 于点 , , ,求 的值.

如图,在 中, , 平分 交 于点 ,点 在 上, , 是 的外接圆,交 于点 .
(1)求证: 是 的切线;
(2)若 的半径为5, ,求 .

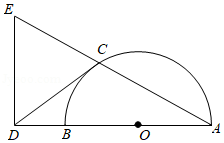
如图,已知点 是以 为直径的半圆上一点, 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,连结 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
如图,在 中, , 是 的平分线,以 为直径的 交 边于点 ,连接 ,过点 作 ,交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
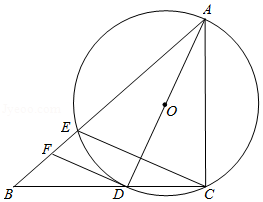
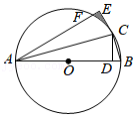
如图, AB是⊙ O的直径,点 F在⊙ O上,∠ BAF的平分线 AE交⊙ O于点 E,过点 E作 ,交 AF的延长线于点 D,延长 DE、 AB相交于点 C.
(1)求证: CD是⊙ O的切线;
(2)若⊙ O的半径为5, ,求 BC的长.

如图, 是 的直径, 为 上一点 不与点 , 重合)连接 , ,过点 作 ,垂足为点 .将 沿 翻折,点 落在点 处得 , 交 于点 .
(1)求证: 是 的切线;
(2)若 , ,求阴影部分面积.
如图, 为 的直径, 为 上一点,连接 , , 为 延长线上一点,连接 ,且 .
(1)求证: 是 的切线;
(2)若 的半径为 , 的面积为 ,求 的长;
(3)在(2)的条件下, 为 上一点,连接 交线段 于点 ,若 ,求 的长.

如图,在圆 中,弦 等于弦 ,且相交于点 ,其中 、 为 、 中点.
(1)证明: ;
(2)连接 、 、 ,若 ,证明:四边形 为矩形.

如图, 是 的直径,点 、 在 上,且 ,连接 、 ,过点 作 的切线,分别与 、 的延长线交于点 、 .
(1)求证: ;
(2)若 , ,求线段 的长.
