有两个内角分别是它们对角的一半的四边形叫做半对角四边形.
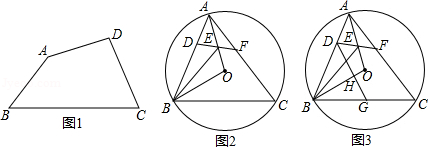
(1)如图1,在半对角四边形 中, , ,求 与 的度数之和;
(2)如图2,锐角 内接于 ,若边 上存在一点 ,使得 , 的平分线交 于点 ,连接 并延长交 于点 , .求证:四边形 是半对角四边形;
(3)如图3,在(2)的条件下,过点 作 于点 ,交 于点 ,当 时,求 与 的面积之比.
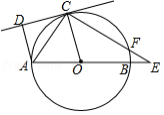
如图,在 中, ,以 为直径的 交 于点 ,切线 交 于点 .
(1)求证: ;
(2)若 , ,求 的长.

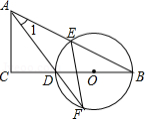
如图,已知: 是 的直径,点 在 上, 是 的切线, 于点 , 是 延长线上一点, 交 于点 ,连接 、 .
(1)求证: 平分 .
(2)若 ,
①求 的度数;
②若 的半径为 ,求线段 的长.
如图,已知 , .
(1)在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);
(2)连接 , ,求 的度数.

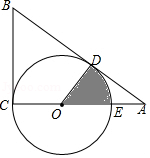
如图, 为 的直角边 上一点,以 为半径的 与斜边 相切于点 ,交 于点 .已知 , .
(1)求 的长;
(2)求图中阴影部分的面积.
如图,已知 内接于 ,点 在劣弧 上(不与点 , 重合),点 为弦 的中点, , 与 的延长线交于点 ,射线 与射线 交于点 ,与 交于点 ,设 , , ,
(1)点点同学通过画图和测量得到以下近似数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
猜想: 关于 的函数表达式, 关于 的函数表达式,并给出证明;
(2)若 , , 的面积为 的面积的4倍,求 半径的长.

如图,在射线 , , , 围成的菱形 中, , , 是射线 上一点, 与 , 都相切,与 的延长线交于点 .过 作 交线段 (或射线 于点 ,交线段 (或射线 于点 .以 为边作矩形 ,点 , 分别在围成菱形的另外两条射线上.
(1)求证: .
(2)设 ,当矩形 的面积为 时,求 的半径.
(3)当 或 与 相切时,求出所有满足条件的 的长.

如图,在 中, , 是 边上一点,以 为直径的 经过 的中点 ,交 的延长线于点 ,连接 .
(1)求证: .
(2)若 , ,求 的长.
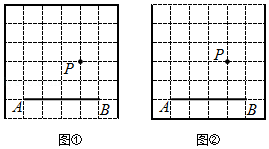
如图,在方格纸中,点 , , 都在格点上.请按要求画出以 为边的格点四边形,使 在四边形内部(不包括边界上),且 到四边形的两个顶点的距离相等.
(1)在图甲中画出一个 .
(2)在图乙中画出一个四边形 ,使 ,且 .(注:图甲、乙在答题纸上)
如图, 为 的直径,弦 ,垂足为点 ,直线 与 的延长线交于点 ,且 .
(1)求证:直线 是 的切线.
(2)若 , ,求线段 的长.

如图,已知 的直径 ,弦 , 的平分线交 于点 ,过点 作 交 的延长线于点 .
(1)求证: 是 的切线.
(2)求 的长.

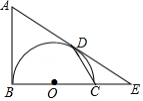
如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
如图, 是以 为直径的半圆 的切线, 为半圆上一点, , , 的延长线相交于点 .
(1)求证: 是半圆 的切线;
(2)连接 ,求证: ;
(3)若 , ,求 的长.
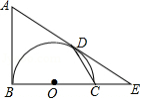
四边形 的对角线交于点 ,有 , ,以 为直径的半圆过点 ,圆心为 .
(1)利用图1,求证:四边形 是菱形.
(2)如图2,若 的延长线与半圆相切于点 ,已知直径 .
①连接 ,求 的面积.
②求弧 的长.
