如图,E是矩形ABCD的边CD上的一点,BE交AC于点O,已知△OCE和△OBC的面积分别为2和8.
(1)求△OAB和四边形AOED的面积;
(2)若BE⊥AC,求BE的长.
如图所示,在长和宽分别是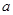 、
、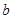 的矩形纸片的四个角都剪去一个边长为
的矩形纸片的四个角都剪去一个边长为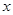 的小正方形.
的小正方形.
(1)用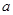 、
、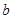 、
、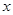 表示纸片剩余部分的面积;
表示纸片剩余部分的面积;
(2)当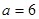 ,
,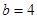 ,且剪去部分的面积等于剩余部分的面积时,求正方形的边长
,且剪去部分的面积等于剩余部分的面积时,求正方形的边长 的值.
的值.
(材料阅读)
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1中的 .人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角 的大小是变化的.
(实际应用)
观测点 在图1所示的 上,现在利用这个工具尺在点 处测得 为 ,在点 所在子午线往北的另一个观测点 ,用同样的工具尺测得 为 . 是 的直径, .
(1)求 的度数;
(2)已知
,求这两个观测点之间的距离即
上
的长.
取

问题:已知 、 均为锐角, , ,求 的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为 ,请借助这个网格图求出 的度数;
延伸:(2)设经过图中 、 、 三点的圆弧与 交于 ,求 的弧长.

如图, 为 的直径, 为 上一点,经过点 的切线交 的延长线于点 , 交 的延长线于点 , 交 于 , 于 ,分别交 、 于 、 ,连接 , .
(1)求证: 平分 ;
(2)若 , ,
①求 的半径;
②求 的长.

如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=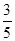 .求证:CB是⊙O的切线.
.求证:CB是⊙O的切线.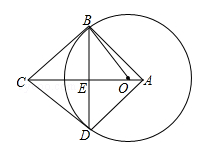
如图,在四边形 中, , , ,以点 为圆心, 为半径的圆与 相切于点 ,交 于点
(1)求 的大小及 的长度;
(2)在 的延长线上取一点 ,使得 上的一个动点 到点 的最短距离为 ,求 的长.

已知:如图,在□ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF;
(2)当∠DOE满足什么条件时,四边形BEDF是菱形,说明理由.
如图,在正方形ABCD中AC与BD交于点O,形外有一点E,使∠AED=90°,且DE=3,OE= ,则AE= .
,则AE= .
如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
在矩形 中,
中, ,
, ,点
,点 从点
从点 沿矩形的边以
沿矩形的边以 的速度经
的速度经 向
向 运动,点
运动,点 从
从 点出发沿矩形的边以
点出发沿矩形的边以 的速度经
的速度经 向
向 运动,点
运动,点 、
、 同时运动,且一点到达终点另一点也停止运动,求几秒后以
同时运动,且一点到达终点另一点也停止运动,求几秒后以 、
、 、
、 为顶点的三角形的面积等于6平方厘米?
为顶点的三角形的面积等于6平方厘米?
两组邻边分别相等的四边形我们称它为筝形.
如图,在筝形 中,
中, ,
, ,
, ,
, 相交于点
相交于点 ,
,
(1)求证:① ;
;
② ,
, ;
;
(2)如果 ,
, ,求筝形
,求筝形 的面积.
的面积.