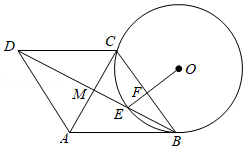
如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过 作 于点 ,交 的延长线于点 ,过点 作 于 .
(1)求证: ;
(2)求证:直线 是 的切线.

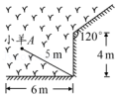
如图,一根 长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊 (羊只能在草地上活动)那么小羊 在草地上的最大活动区域面积是
| A. |
|
B. |
|
C. |
|
D. |
|
如图是一位同学从照片上剪切下来的海上日出时的画面,"图上"太阳与海平线交于 , 两点,他测得"图上"圆的半径为10厘米, 厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则"图上"太阳升起的速度为

| A. |
1.0厘米 分 |
B. |
0.8厘米 分 |
C. |
1.2厘米 分 |
D. |
1.4厘米 分 |
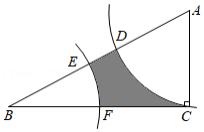
如图,在 中, , , ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为
| A. |
|
B. |
|
C. |
|
D. |
|
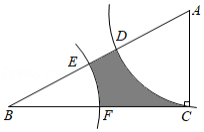
如图,在 中, , , ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为
A. B. C. D.
如图, 是 的直径,过点 作 的切线 ,点 是射线 上的动点,连接 ,过点 作 ,交 于点 ,连接 .
(1)求证: 是 的切线;
(2)当四边形 是平行四边形时,求 的度数.

已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 .(用含 的代数式表示),圆心角为 度.
如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径 ,根据我国魏晋时期数学家刘徽的"割圆术"思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计 的值,下面 及 的值都正确的是

| A. |
, |
| B. |
, |
| C. |
, |
| D. |
, |
如图,在菱形 中,对角线 、 相交于点 , 经过点 , ,交对角线 于点 ,且 ,连接 交 于点 .
(1)试判断 与 的位置关系,并说明理由;
(2)若 , ,求 的半径.