初中数学圆试题

如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP⊥AB交边CD于点P，连接NM，NP．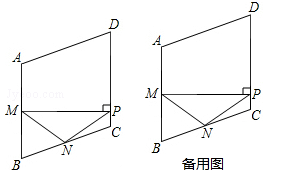

（1）若∠B=60°，这时点P与点C重合，则∠NMP=       度；
（2）求证：NM=NP；
（3）当△NPC为等腰三角形时，求∠B的度数．

如图1，在□ABCD中，BD＝4，将□ABCD绕其对称中心O旋转90°，则点D经过的路径长为(      )

A．4π

B．3π

C．2π

D．π

如图，在矩形ABCD中，AB＝4，BC＝6，E为AB中点，动点P从点B开始沿BC方向运动到点C停止，动点Q从点C开始沿CD—DA方向运动，点Q与点P同时出发，当有一个动点到达终点时，两点的运动同时停止．这两点的运动速度均为每秒1个单位．若设他们的运动时间为x（秒），△EPQ的面积为y，则y与x之间的函数关系的图像大致是(      )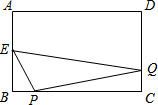

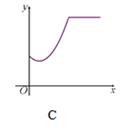
如图，已知E、F是□ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC.
求证： BE=DF；                           

菱形的两条对角线长分别是6和8，则此菱形的边长是（ ）

A．10

B．8

C．6

D．5

矩形具有而菱形不一定具有的性质是               (     )

A．对角线互相垂直

B．对角线相等

C．对角线互相平分

D．对角互补

一个八边形的内角和是      .

如图，四边形 $\mathit{ABCD}$ 是 $\odot O$ 的内接四边形， $\mathit{BE}$ 是 $\odot O$ 的直径，连接 $\mathit{AE}$ ．若 $\angle \mathit{BCD}=2\angle \mathit{BAD}$ ，则 $\angle \mathit{DAE}$ 的度数是 $($ 　　 $)$

A．

$30°$

B．

$35°$

C．

$45°$

D．

$60°$

已知正n边形的每一个内角都等于144°，则n为（ ）

A．9

B．10

C．12

D．15

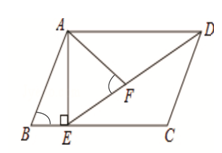
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．若AB=8，AD=6，AF=4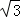，则AE的长为                   ．

点O是△ABC的外心，若∠BOC=80°，则∠BAC的度数为（   ）

A．40°

B．100°

C．40°或140°

D．40°或100°

已知正方形ABCD的一条对角线长为2，则它的面积是（    ）

A．2

B．4

C．6

D．12

若正方形的对角线长为2 cm，则这个正方形的面积为（    ）

A．4cm^2

B．2cm^2

C．cm^2

D．2cm^2

下列命题中错误的是（ ）．

A．平行四边形的对角线互相平分

B．菱形的对角线互相垂直

C．同旁内角互补

D．矩形的对角线相等

如图，已知DE是△ABC的中位线，=4，则=_____