初中数学圆试题

如图1，在□ABCD中，AH⊥DC，垂足为H，AB=4，AD=7，AH=．现有两个动点E，F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动，在点E，F的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，点G在射线AB上，当点E运动到点C时，E，F两点同时停止运动，设运动时间为t秒．
    
（1）试求出当点G与点B重合时t的值；
（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请求出S与t之间的函数表达式，并写出相应的自变量t的取值范围；
（3）当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度α（0°＜α＜360°），在旋转过程中，点E与点C重合，F的对应点为F′，G的对应点为G′，设直线F′G′与射线DC、射线AC分别相交于M，N两点．试问：是否存在点M，N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出CM的长度；若不存在，请说明理由．

如果一个多边形的内角和是1440⁰，那么这个多边形的边数是        ．

将等边三角形、正方形、正五边形按如图所示的位置摆放，如果∠1=41°，∠2=51°，那么∠3的度数等于      ．

如图，□ABCD中，点E是AD边的中点，BE交对角线AC于点F，若AF=2，则对角线AC长为             .

如图，△ABC是等腰三角形，AB＝BC，点D为BC的中点．

（1）用圆规和没有刻度的直尺作图，并保留作图痕迹：
①过点B作AC的平行线BP；
②过点D作BP的垂线，分别交AC，BP，BQ于点E，F，G．
（2）在（1）所作的图中，连接BE，CF．求证：四边形BFCE是平行四边形．

一个多边形的内角是1440°，求这个多边形的边数是（   ）

A．7

B．8

C．9

D．10

若一个正方形的面积为8，则这个正方形的边长为（ ）

A．4

B．2

C．

D．8

如图，四边形 $\mathit{ABCD}$ 是 $\odot O$ 的内接四边形， $\mathit{BE}$ 是 $\odot O$ 的直径，连接 $\mathit{AE}$ ．若 $\angle \mathit{BCD}=2\angle \mathit{BAD}$ ，则 $\angle \mathit{DAE}$ 的度数是 $($ 　　 $)$

A．

$30°$

B．

$35°$

C．

$45°$

D．

$60°$

已知正n边形的每一个内角都等于144°，则n为（ ）

A．9

B．10

C．12

D．15

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．若AB=8，AD=6，AF=4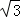，则AE的长为                   ．

点O是△ABC的外心，若∠BOC=80°，则∠BAC的度数为（   ）

A．40°

B．100°

C．40°或140°

D．40°或100°

已知正方形ABCD的一条对角线长为2，则它的面积是（    ）

A．2

B．4

C．6

D．12

若正方形的对角线长为2 cm，则这个正方形的面积为（    ）

A．4cm^2

B．2cm^2

C．cm^2

D．2cm^2

下列命题中错误的是（ ）．

A．平行四边形的对角线互相平分

B．菱形的对角线互相垂直

C．同旁内角互补

D．矩形的对角线相等

如图，已知DE是△ABC的中位线，=4，则=_____