如图,在四边形ABCD中,点E、F是BC、CD的中点,且AE⊥BC,AF⊥CD.
(1)求证:AB=AD.
(2)请你探究∠EAF,∠BAE,∠DAF之间有什么数量关系?并证明你的结论.
如图,为
的直径,
为
上的一点,
,
,
的延长线交
于点
,连接
.
(1)求证:是
的切线;
(2)若为
的中点,求
的值.
如图,在 中, , 为 的中点, 与半圆 相切于点 .
(1)求证: 是半圆 所在圆的切线;
(2)若 , ,求半圆 所在圆的半径.

如图,在等腰中,
,以
为直径作
交
于点
,过点
作
,垂足为
.
(1)求证:是
的切线.
(2)若,
,求
的长.

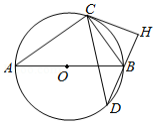
如图,已知 是 的直径, 是 延长线上一点, 切 于点 , 是 的弦, ,垂足为 .
(1)求证: .
(2)过点 作 交 于点 ,交 于点 ,连接 ,若 , ,求 的长.

如图,在中,
.
(1)已知线段的垂直平分线与
边交于点
,连接
,求证:
.
(2)以点为圆心,线段
的长为半径画弧,与
边交于点
,连接
.若
,求
的度数.

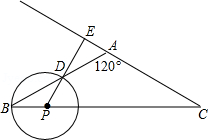
如图, 中, , . 是底边 上的一个动点 与 、 不重合),以 为圆心, 为半径的 与射线 交于点 ,射线 交射线 于点 .
(1)若点 在线段 的延长线上,设 , ,求 关于 的函数关系式,并写出 的取值范围.
(2)当 时,试说明射线 与 是否相切.
(3)连接 ,若 ,求 的长.
(贵州省安顺市)(本题12分)
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求 的值.
的值.
请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德 ,公元前 公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据 译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1, 和 是 的两条弦(即折线 是圆的一条折弦), , 是 的中点,则从 向 所作垂线的垂足 是折弦 的中点,即 .下面是运用"截长法"证明 的部分证明过程.证明:如图2,在 上截取 ,连接 , , 和 .
是 的中点,
.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边 内接于 , , 为 上一点, , 于点 ,则 的周长是 .
如图,在中,
,点
在
上,以
为半径作
,与
相交于点
,与
相切于点
,过点
作
,垂足为
.
(1)求证:是
的切线;
(2)若,
,求
的半径.

如图,在 中, ,点 在 上.
(1)求作: ,使点 在 上,且 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若 .求证: .

如图,一次函数 与反比例函数 的图象交于点 , .
(1)求这两个函数的表达式;
(2)在 轴上是否存在点 , ,使 为等腰三角形?若存在,求 的值;若不存在,说明理由.

如图,已知 是 的直径,过 点作 ,交弦 于点 ,交 于点 ,且使 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

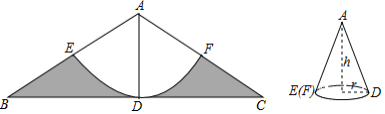
如图,在等腰中,
,
是
的角平分线,且
,以点
为圆心,
长为半径画弧
,交
于点
,交
于点
.
(1)求由弧及线段
、
、
围成图形(图中阴影部分)的面积;
(2)将阴影部分剪掉,余下扇形,将扇形
围成一个圆锥的侧面,
与
正好重合,圆锥侧面无重叠,求这个圆锥的高
.