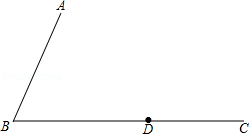中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
如图,平行四边形 的对角线 、 相交于点 , 平分 ,分别交 、 于点 、 ,连接 , , ,则下列结论:
① ② ③ ④ ⑤ ,正确的个数是

A.2B.3C.4D.5
如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上.
(1)在图中画出以线段 为一边的矩形 (不是正方形),且点 和点 均在小正方形的顶点上;
(2)在图中画出以线段 为一腰,底边长为 的等腰三角形 ,点 在小正方形的顶点上,连接 ,请直接写出线段 的长.

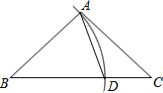
如图,以 的顶点 为圆心, 长为半径画弧,交 边于点 ,连接 .若 , ,则 的大小为 度.
如图,在 中, ,以点 为圆心, 长为半径画弧,交 于点 和点 ,再分别以点 , 为圆心,大于 长为半径画弧,两弧相交于点 ,作射线 交 于点 .若 , ,则 的长度是

A.2B.3C. D.
请认真阅读下面的数学小探究系列,完成所提出的问题:
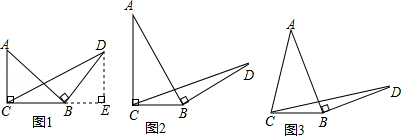
(1)探究1:如图1,在等腰直角三角形 中, , ,将边 绕点 顺时针旋转 得到线段 ,连接 .求证: 的面积为 .(提示:过点 作 边上的高 ,可证 )
(2)探究2:如图2,在一般的 中, , ,将边 绕点 顺时针旋转 得到线段 ,连接 .请用含 的式子表示 的面积,并说明理由.
(3)探究3:如图3,在等腰三角形 中, , ,将边 绕点 顺时针旋转 得到线段 ,连接 .试探究用含 的式子表示 的面积,要有探究过程.
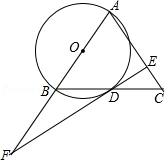
如图,在 中, ,以 为直径作 交 于点 ,过点 作 的切线 交 于点 ,交 延长线于点 .
(1)求证: ;
(2)若 , ,求 的长.
已知等腰三角形的腰和底的长分别是一元二次方程 的根,则该三角形的周长为
A.8B.10C.8或10D.12
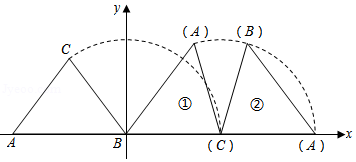
等腰三角形 在平面直角坐标系中的位置如图所示,已知点 ,点 在原点, ,把等腰三角形 沿 轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置② 依此规律,第15次翻转后点 的横坐标是 .
已知:如图, ,射线 上一点 .
求作:等腰 ,使线段 为等腰 的底边,点 在 内部,且点 到 两边的距离相等.