作图题:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹).
已知在平面直角坐标系中(如图),已知抛物线
经过点
,对称轴是直线
,顶点为
.
(1)求这条抛物线的表达式和点的坐标;
(2)点在对称轴上,且位于顶点上方,设它的纵坐标为
,联结
,用含
的代数式表示
的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点在
轴上.原抛物线上一点
平移后的对应点为点
,如果
,求点
的坐标.
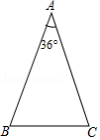
如图,已知等腰 顶角 .
(1)在 上作一点 ,使 (要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加黑);
(2)求证: 是等腰三角形.
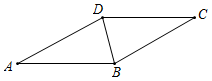
如图,已知 的中垂线
的中垂线 交
交 于点
于点 ,交
,交 于点
于点 ,有下面3个结论:
,有下面3个结论:
① 是等腰三角形;
是等腰三角形;
② ∽
∽ ;
;
③点D是线段AC的黄金分割点.
请你从以上结论中只选一个加以证明
如图,已知锐角 中, .

(1)请在图1中用无刻度的直尺和圆规作图:作 的平分线 ;作 的外接圆 ;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若 , 的半径为5,则 .(如需画草图,请使用图
如图,已知△ABC,用直尺(没有刻度)和圆规在平面上求作一个点P,使P到∠A两边的距离相等,且PA=PB.(不要求写作法,但要保留作图痕迹)
如图,在Rt△ABC中, .
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹:
①作∠ACB的平分线,交斜边AB于点D;
②过点D作AC的垂线,垂足为点E.
(2)在(1)作出的图形中,若 , ,则DE= .

两个城镇 , 与一条公路 ,一条河流 的位置如图所示,某人要修建一避暑山庄,要求该山庄到 , 的距离必须相等,到 和 的距离也必须相等,且在 的内部,请画出该山庄的位置 .(不要求写作法,保留作图痕迹.

如图, BD是菱形 ABCD的对角线,∠ CBD=75°,
(1)请用尺规作图法,作 AB的垂直平分线 EF,垂足为 E,交 AD于 F;(不要求写作法,保留作图痕迹)
(2)在(1)条件下,连接 BF,求∠ DBF的度数.
如图1,在 中, , ,点 , 分别在边 , 上,且 ,连接 .现将 绕点 顺时针方向旋转,旋转角为 ,如图2,连接 , , .
(1)当 时,求证: ;
(2)如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;
(3)在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.

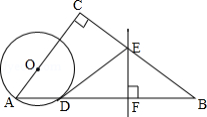
如图,在 中, ,点 在 上,以 为半径的 交 于点 , 的垂直平分线交 于点 ,交 于点 ,连接 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , , ,求线段 的长.
如图,在△ ABC中, BD、 CE分别是 AC、 AB上的中线, BD与 CE相交于点 O.
(1)利用尺规作图取线段 CO的中点.(保留作图痕迹,不写作法);
(2)猜想 CO与 OE的长度有什么关系,并说明理由.

如图,在矩形ABCD中,AB=10,AD=6,点M为AB上的一动点,将矩形ABCD沿某一直线对折,使点C与点M重合,该直线与AB(或BC)、CD(或DA)分别交于点P、Q
(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)
(2)如果PQ与AB、CD都相交,试判断△MPQ的形状并证明你的结论;
(3)设AM=x,d为点M到直线PQ的距离,y=d2,
①求y关于x的函数解析式,并指出x的取值范围;
②当直线PQ恰好通过点D时,求点M到直线PQ的距离.

问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于 ,那么它所对的直角边等于斜边的一半.即:如图1,在 中, , ,则: .
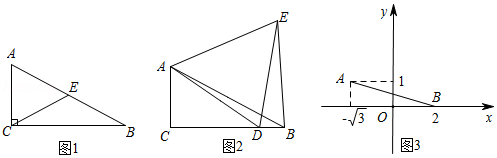
探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接 边上中线 ,由于 ,易得结论:① 为等边三角形;② 与 之间的数量关系为 .
(2)如图2,点 是边 上任意一点,连接 ,作等边 ,且点 在 的内部,连接 .试探究线段 与 之间的数量关系,写出你的猜想并加以证明.
(3)当点 为边 延长线上任意一点时,在(2)条件的基础上,线段 与 之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系 中,点 的坐标为 , ,点 是 轴正半轴上的一动点,以 为边作等边 ,当 点在第一象限内,且 时,求 点的坐标.