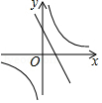
一次函数 与反比例函数 的图象如图所示,则二次函数 的大致图象是
| A. |
|
B. |
|
| C. |
|
D. |
|
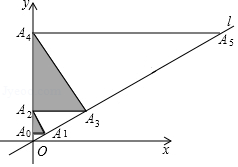
如图,过点 作 轴的垂线交直线 于点 ,过点 作直线 的垂线,交 轴于点 ,过点 作 轴的垂线交直线 于点 , ,这样依次下去,得到△ ,△ ,△ , ,其面积分别记为 , , , ,则 为
| A. |
|
B. |
|
C. |
|
D. |
|
一次函数 的图象经过的象限是
| A. |
一、二、三 |
B. |
二、三、四 |
C. |
一、三、四 |
D. |
一、二、四 |
函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
和
的图象如图所示.
0 |
1 |
2 |
3 |
||||||
0 |
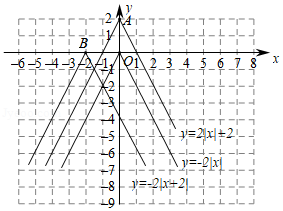
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点,
的坐标和函数
的对称轴.
(2)探索思考:平移函数的图象可以得到函数
和
的图象,分别写出平移的方向和距离.
(3)拓展应用:在所给的平面直角坐标系内画出函数的图象.若点
,
和
,
在该函数图象上,且
,比较
,
的大小.
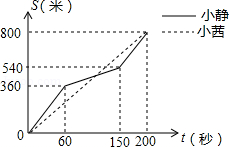
为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程(米
与所用的时间
(秒
之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第 秒.
某物流公司引进、
两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,
种机器人于某日0时开始搬运,过了1小时,
种机器人也开始搬运,如图,线段
表示
种机器人的搬运量
(千克)与时间
(时
的函数图象,线段
表示
种机器人的搬运量
(千克)与时间
(时
的函数图象.根据图象提供的信息,解答下列问题:
(1)求关于
的函数解析式;
(2)如果、
两种机器人连续搬运5个小时,那么
种机器人比
种机器人多搬运了多少千克?

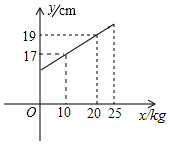
在所挂物体质量不超过时,一弹簧的长度
是所挂物体质量
的一次函数,其图象如图所示.
(1)求与
之间的函数表达式及该弹簧不挂物体时的长度;
(2)若该弹簧挂上一个物体后,弹簧长度为,求这个物体的质量.
设一次函数 的图象经过点 ,且 的值随 的值增大而增大,则该一次函数的图象一定不经过
| A. |
第一象限 |
B. |
第二象限 |
C. |
第三象限 |
D. |
第四象限 |
如图,过点 的两条直线 , 分别交 轴于点 , ,其中点 在原点上方,点 在原点下方,已知 .
(1)求点 的坐标;
(2)若 的面积为4,求直线 的解析式.

已知抛物线 与反比例函数 的图象在第一象限有一个公共点,其横坐标为1,则一次函数 的图象可能是
| A. |
|
B. |
|
C. |
|
D. |
|
有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量有两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.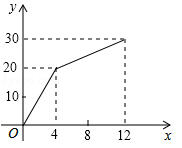
(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
(年青海省中考)已知一次函数 与反比例函数
与反比例函数 ,那么它们在同一坐标系中的图象可能是( )
,那么它们在同一坐标系中的图象可能是( )
A. |
B. |
C. |
D. |