探究函数性质时,我们经历了列表、描点、连线画函数图象,观察分析图象特征,概括函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
6 |
5 |
4 |
|
2 |
1 |
|
7 |
|
(1)写出函数关系式中 及表格中 , 的值:
, , ;
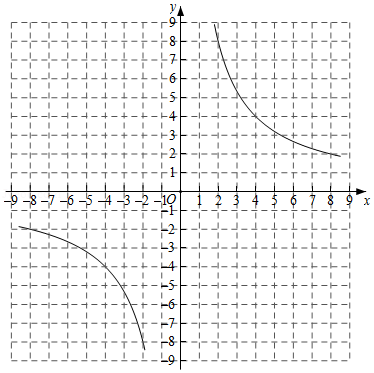
(2)根据表格中的数据在所给的平面直角坐标系中画出该函数的图象,并根据图象写出该函数的一条性质: ;
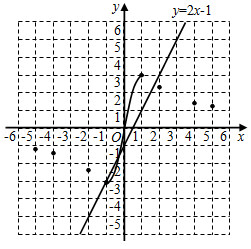
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.
在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质及其应用的过程.以下是我们研究函数 的性质及其应用的部分过程,请按要求完成下列各小题.
(1)请把下表补充完整,并在给出的图中补全该函数的大致图象;
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
0 |
|
4 |
|
0 |
|
|
|
|
(2)请根据这个函数的图象,写出该函数的 条性质;
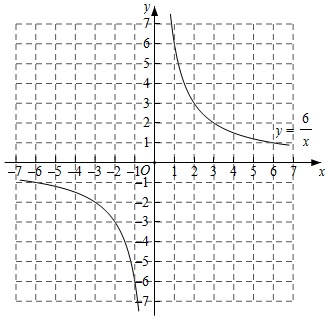
(3)已知函数 的图象如图所示.根据函数图象,直接写出不等式 的解集.(近似值保留一位小数,误差不超过
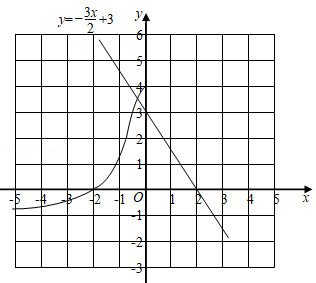
)已知正比例函数 与反比例函数 的图象都经过点 .
(1)求 , 的值;
(2)在图中画出正比例函数 的图象,并根据图象,写出正比例函数值大于反比例函数值时 的取值范围.
甲、乙两人沿同一直道从 地去 地.甲比乙早 出发,乙的速度是甲的2倍.在整个行程中,甲离 地的距离 (单位: 与时间 (单位: 之间的函数关系如图所示.
(1)在图中画出乙离 地的距离 (单位: 与时间 之间的函数图象;
(2)若甲比乙晚 到达 地,求甲整个行程所用的时间.

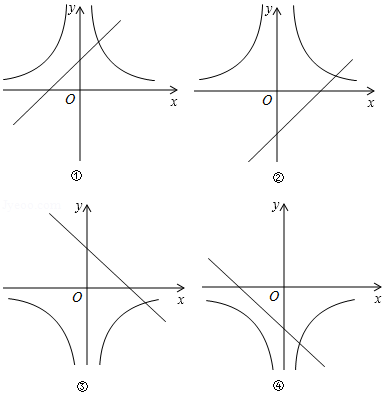
在同一直角坐标系中,函数 与 的大致图象是
| A. |
①② |
B. |
②③ |
C. |
②④ |
D. |
③④ |
在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.
(1)请把下表补充完整,并在图中补全该函数图象;
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
(2)根据函数图象,判断下列关于该函数性质的说法是否正确,正确的在答题卡上相应的括号内打“ ”,错误的在答题卡上相应的括号内打“ ”;
①该函数图象是轴对称图形,它的对称轴为 轴.
②该函数在自变量的取值范围内,有最大值和最小值.当 时,函数取得最大值3;当 时,函数取得最小值 .
③当 或 时, 随 的增大而减小;当 时, 随 的增大而增大.
(3)已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集(保留1位小数,误差不超过 .
如图,一个弹簧不挂重物时长 ,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长 (单位: 关于所挂物体质量 (单位: 的函数图象如图所示,则图中 的值是
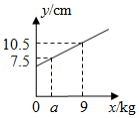
A.3B.4C.5D.6
某通讯公司就上宽带网推出 , , 三种月收费方式.这三种收费方式每月所需的费用 (元 与上网时间 的函数关系如图所示,则下列判断错误的是

A.每月上网时间不足 时,选择 方式最省钱
B.每月上网费用为60元时, 方式可上网的时间比 方式多
C.每月上网时间为 时,选择 方式最省钱
D.每月上网时间超过 时,选择 方式最省钱
如图,直线 与 轴, 轴分别交于 、 两点, 与△ 是以点 为位似中心的位似图形,且相似比为 ,则点 的坐标为 .

小慧根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数 的自变量 的取值范围是 ;
(2)列表,找出 与 的几组对应值.
|
|
|
0 |
1 |
2 |
3 |
|
|
|
b |
1 |
0 |
1 |
2 |
|
其中, ;
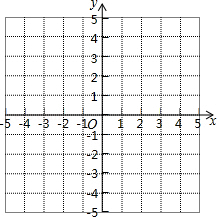
(3)在平面直角坐标系 中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质: .
在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线 与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则 的取值范围是
A. B. C. D. 且