初中数学平面直角坐标系试题

在平面直角坐标系中，一个智能机器人接到如下指令：从原点 O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1 m．其行走路线如图所示，第1次移动到 A ₁，第2次移动到 A ₂，…，第 n次移动到 A _n．则△ OA ₂ A ₂₀₁₈的面积是（　　）

A．

504m ^2

B．

$\frac{1009}{2}$ m ^2

C．

$\frac{1011}{2}$ m ^2

D．

1009m ^2

已知正方形的对称中心在坐标原点，顶点 A、 B、 C、 D按逆时针依次排列，若 A点的坐标为（2， $\sqrt{3}$ ），则 B点与 D点的坐标分别为（　　）

A．	（﹣2， $\sqrt{3}$ ），（2，﹣ $\sqrt{3}$ ）	B．	（﹣ $\sqrt{3}$ ，2），（ $\sqrt{3}$ ，﹣2）
C．	（﹣ $\sqrt{3}$ ，2），（2，﹣ $\sqrt{3}$ ）	D．	（- $\frac{\sqrt{7}}{2}$ ， $\frac{\sqrt{21}}{2}$ ）（ $\frac{\sqrt{7}}{2}$ ， $-\frac{\sqrt{21}}{2}$ ）

如图，在平面直角坐标系中，已知 A（﹣1，0）， B（0，2），将△ ABO沿直线 AB翻折后得到△ ABC，若反比例函数 y＝ $\frac{k}{x}$ （ x＜0）的图象经过点 C，则 k＝ 　　．

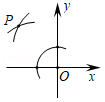
如图，在平面直角坐标系中，以 O为圆心，适当长为半径画弧，交 x轴于点 M，交 y轴于点 N，再分别以点 M， N为圆心，大于 MN的长为半径画弧，两弧在第二象限交于点 P，若点 P的坐标为（3 a， b+1），则 a与 b的数量关系为（　　）

A．

3a＝2b

B．

3a＝b+1

C．

3a+b﹣1＝0

D．

3a＝﹣b﹣1

下列运算及判断正确的是（　　）

A．	﹣5× $\frac{1}{5}$ ÷（﹣ $\frac{1}{5}$ ）×5＝1
B．	方程（x ^2+x﹣1） ^x ^+3＝1有四个整数解
C．	若a×567 ^3＝10 ^3，a÷10 ^3＝b，则a×b＝ $\frac{{10}^3}{{567}^6}$
D．	有序数对（m ^2+1，|m|）在平面直角坐标系中对应的点一定在第一象限

在平面直角坐标系中，对于点 P（ a， b），我们把 Q（﹣ b+1， a+1）叫做点 P的伴随点，已知 A ₁的伴随点为 A ₂， A ₂的伴随点为 A ₃，…，这样依次下去得到 A ₁， A ₂， A ₃，…， A _n，若 A ₁的坐标为（3，1），则 A ₂₀₁₈的坐标为 　　．

平面直角坐标系中，已知 $A（2，2\mathit{）、}B（4，0）$．若在坐标轴上取点C，使△ABC为等腰三角形，则满足条件的点C的个数是（　　）

A．5B．6C．7D．8

若点 $M（k﹣1，k+1）$关于y轴的对称点在第四象限内，则一次函数 $y\mathit{＝（}k﹣1）x+k$的图象不经过第　　象限．

在平面直角坐标系中，若点A（a，﹣b）在第一象限内，则点B（a，b）所在的象限是（　　）

A．第一象限B．第二象限C．第三象限D．第四象限

如图，在矩形OABC纸片中，OA＝7，OC＝5，D为BC边上动点，将△OCD沿OD折叠，当点C的对应点落在直线l：y＝﹣x+7上时，记为点E，F，当点C的对应点落在边OA上时，记为点G．

（1）求点E，F的坐标；

（2）求经过E，F，G三点的抛物线的解析式；

（3）当点C的对应点落在直线l上时，求CD的长；

（4）在（2）中的抛物线上是否存在点P，使以E，F，P为顶点的三角形是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

如图，直线l： $y=-\frac{4}{3}x$，点A₁坐标为（﹣3，0）．过点A₁作x轴的垂线交直线l于点B₁，以原点O为圆心，OB₁长为半径画弧交x轴负半轴于点A₂，再过点A₂作x轴的垂线交直线l于点B₂，以原点O为圆心，OB₂长为半径画弧交x轴负半轴于点A₃，…，按此做法进行下去，点A₂₀₁₆的坐标为　　．

如图，在平面直角坐标系中， $\Delta A_1{A}_2{A}_3，\Delta A_3{A}_4{A}_5，\Delta A_5{A}_6{A}_7，\Delta A_7{A}_8{A}_9，$…，都是等边三角形，且点A₁，A₃，A₅，A₇，A₉的坐标分别为 $A_1（3,0\mathit{），}{A}_3（1,0\mathit{），}{A}_5（4,0\mathit{），}{A}_7（0,0\mathit{），}{A}_9（5,0）$，依据图形所反映的规律，则A₁₀₀的坐标为　    　．

如图，以正六边形 ABCDEF的中心为坐标原点建立平面直角坐标系，顶点 C、 F在 x轴上，顶点 A的坐标为（1， ），则顶点 D的坐标为 　 　．

已知平行四边形 ABCD的顶点 A在第三象限，对角线 AC的中点在坐标原点，一边 AB与 x轴平行且 AB＝2，若点 A的坐标为（ a， b），则点 D的坐标为 　．

在平面直角坐标系中，点 P（ x， y）经过某种变换后得到点 P'（﹣ y+1， x+2），我们把点 P'（﹣ y+1， x+2）叫做点 P（ x， y）的终结点．已知点 P ₁的终结点为 P ₂，点 P ₂的终结点为 P ₃，点 P ₃的终结点为 P ₄，这样依次得到 P ₁、 P ₂、 P ₃、 P ₄、… P _n、…，若点 P ₁的坐标为（2，0），则点 P ₂₀₁₇的坐标为 　　．