在平面直角坐标系中,三个顶点的坐标分别为
,
,
.以原点
为位似中心,把这个三角形缩小为原来的
,得到
,则点
的对应点
的坐标是 .
如图,在平面直角坐标系中,正方形 和正方形 的顶点 , 在 轴上,顶点 , 在 轴上,且 ,反比例函数 的图象经过点 ,则 .

如图,在平面直角坐标系中,直线 与直线 交于点 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 ,过 作 的平行线交 于 ,过 作 轴的垂线,垂足为 按此规律,则点 的纵坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在直角坐标系中,点 , 是第一象限角平分线上的两点,点 的纵坐标为1,且 ,在 轴上取一点 ,连接 , , , ,使得四边形 的周长最小,这个最小周长的值为 .

如图,矩形硬纸片的顶点
在
轴的正半轴及原点上滑动,顶点
在
轴的正半轴及原点上滑动,点
为
的中点,
,
.给出下列结论:①点
从点
出发,到点
运动至点
为止,点
经过的路径长为
;②
的面积最大值为144;③当
最大时,点
的坐标为
,
.其中正确的结论是 .(填写序号)
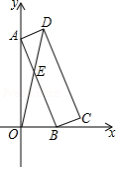
如图,在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,过点 作 轴的垂线交直线 于点 ,过点 作 的垂线交 轴于点 ,此时点 与原点 重合,连接 交 轴于点 ,得到第1个△ ;过点 作 轴的垂线交 于点 ,过点 作 轴的平行线交 于点 ,连接 与 交于点 ,得到第2个△ 按照此规律进行下去,则第2019个△ 的面积是 .

如图,在直角坐标系中,已知点A( ,0)、B(
,0)、B( ,3),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2014的直角顶点的坐标为 。
,3),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2014的直角顶点的坐标为 。

(年江西省南昌市)如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
如图,若抛物线 与 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为 ,则反比例函数 的图象是

| A. |
|
B. |
|
| C. |
|
D. |
|
在平面直角坐标系中, 为原点,点 ,点 ,把 绕点 逆时针旋转,得△ ,点 , 旋转后的对应点为 , ,记旋转角为 .
(Ⅰ)如图①,若 ,求 的长;
(Ⅱ)如图②,若 ,求点 的坐标;
(Ⅲ)在(Ⅱ)的条件下,边 上 的一点 旋转后的对应点为 ,当 取得最小值时,求点 的坐标(直接写出结果即可)

如图,由两个长为2,宽为1的长方形组成“7”字图形

(1)将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形,其中顶点
位于
轴上,顶点
,
位于
轴上,
为坐标原点,则
的值为 .
(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点,摆放第三个“7”字图形得顶点
,依此类推,
,摆放第
个“7”字图形得顶点
,
,则顶点
的坐标为 .
如图,在平面直角坐标系中,我们把横、纵坐标都是整数的点为“整点”,已知点
的坐标为
,点
在
轴的上方,
的面积为
,则
内部(不含边界)的整点的个数为 .
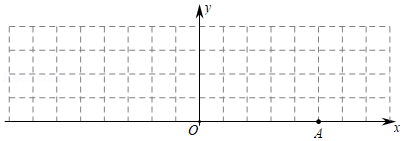
如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是
A. B. C. D.