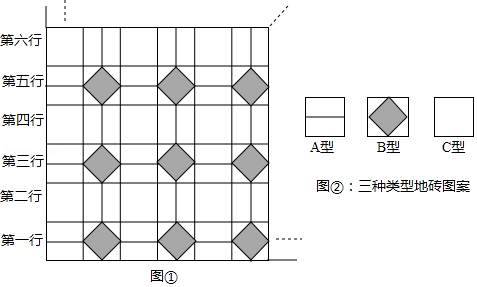
如图①,某广场地面是用 , , 三种类型地砖平铺而成的.三种类型地砖上表面图案如图②所示.现用有序数对表示每一块地砖的位置:第一行的第一块 型)地砖记作 ,第二块 型)地砖记作 若 位置恰好为 型地砖,则正整数 , 须满足的条件是 .
如图,在平面直角坐标系中,有一只用七巧板拼成的"猫",三角形①的边 及四边形②的边 都在 轴上,"猫"耳尖 在 轴上.若"猫"尾巴尖 的横坐标是1,则"猫"爪尖 的坐标是 .

如图,四边形 是矩形,点 的坐标为 ,点 的坐标为 ,把矩形 沿 折叠,点 落在点 处,则点 的坐标为 .

定义:在平面直角坐标系中,一个图形先向右平移 个单位,再绕原点按顺时针方向旋转 角度,这样的图形运动叫作图形的 变换.
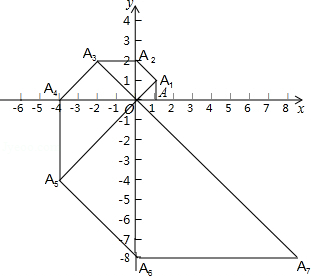
如图,等边 的边长为1,点 在第一象限,点 与原点 重合,点 在 轴的正半轴上.△ 就是 经 变换后所得的图形.
若 经 变换后得△ ,△ 经 变换后得△ ,△ 经 变换后得△ ,依此类推
△ 经 变换后得△ ,则点 的坐标是 ,点 的坐标是 .
现有四张正面分别标有数字 ,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为 , .则点 在第二象限的概率为 .
在平面直角坐标系中,已知 , , ,若线段 与 互相平分,则点 关于坐标原点的对称点的坐标为 .
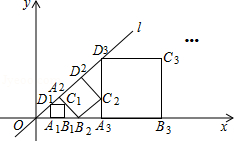
如图,在平面直角坐标系中,直线 为正比例函数 的图象,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线 的垂线,垂足为 ,交 轴于点 ,以 为边作正方形 ;过点 作 轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 , ,按此规律操作下所得到的正方形 的面积是 .
如图,点 、 在反比例函数 的图象上,延长 交 轴于 点,若 的面积是12,且点 是 的中点,则 .

如图,平面直角坐标系中,矩形 的顶点 , , .将矩形 绕点 顺时针方向旋转,使点 恰好落在 上的点 处,则点 的对应点 的坐标为 .

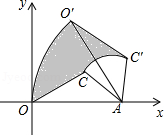
如图, 的顶点 在坐标原点, 边在 轴上, , ,把 绕点 按顺时针方向旋转到△ ,使得点 的坐标是 ,则在旋转过程中线段 扫过部分(阴影部分)的面积为 .
如图,在平面直角坐标系中,等腰直角三角形 的直角边 在 轴上,点 在第一象限,且 ,以点 为直角顶点, 为一直角边作等腰直角三角形 ,再以点 为直角顶点, 为直角边作等腰直角三角形 依此规律,则点 的坐标是 .
已知直角坐标系内有四个点 , , , ,若以 , , , 为顶点的四边形是平行四边形,则 .