如图1,已知矩形 , , ,动点 从点 出发,以 的速度向点 运动,直到点 为止;动点 同时从点 出发,以 的速度向点 运动,与点 同时结束运动.
(1)点 到达终点 的运动时间是 ,此时点 的运动距离是 ;
(2)当运动时间为 时, 、 两点的距离为 ;
(3)请你计算出发多久时,点 和点 之间的距离是 ;
(4)如图2,以点 为坐标原点, 所在直线为 轴, 所在直线为 轴, 长为单位长度建立平面直角坐标系,连接 ,与 相交于点 ,若双曲线 过点 ,问 的值是否会变化?若会变化,说明理由;若不会变化,请求出 的值.

如图,菱形 的边 在 轴上,点 的坐标为 ,点 在反比例函数 的图象上,直线 经过点 ,与 轴交于点 ,连接 , .
(1)求 , 的值;
(2)求 的面积.

如图,在直角坐标系 中,矩形 的顶点 、 分别在 轴和 轴正半轴上,点 的坐标是 ,点 是 边上一动点(不与点 、点 重合),连接 、 ,过点 作射线 交 的延长线于点 ,交 边于点 ,且 ,令 , .
(1)当 为何值时, ?
(2)求 与 的函数关系式,并写出 的取值范围;
(3)在点 的运动过程中,是否存在 ,使 的面积与 的面积之和等于 的面积?若存在,请求 的值;若不存在,请说明理由.

如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上. 且 ,OB,OC的长分别是一元二次方程 的两个根 .
(1)求点A和点B的坐标.
(2)点P是线段OB上的一个动点(点P不与点O,B重合),过点P的直线l与y轴平行,直线l交边OA或边AB于点Q,交边OC或边BC于点R.设点P的横坐标为t,线段QR的长度为m.已知 时,直线l恰好过点C.当 时,求m关于t的函数关系式.
(3)当 时,请直接写出点P的坐标.

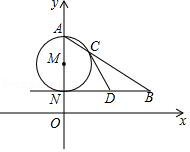
如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线l:y=﹣x+7上时,记为点E,F,当点C的对应点落在边OA上时,记为点G.
(1)求点E,F的坐标;
(2)求经过E,F,G三点的抛物线的解析式;
(3)当点C的对应点落在直线l上时,求CD的长;
(4)在(2)中的抛物线上是否存在点P,使以E,F,P为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.

如图,在平面直角坐标系中, O(0,0), A(0,﹣6), B(8,0)三点在⊙ P上, M为劣弧的 中点.
(1)求圆的半径及圆心 P的坐标;
(2)求证: AM是∠ OAB的平分线;
(3)连接 BM并延长交 y轴于点 N,求 N, M点的坐标.

如图,在平面直角坐标系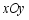 中,已知点
中,已知点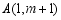 ,
,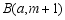 ,
,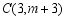 ,
,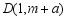 ,
,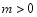 ,
,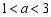 ,点
,点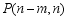 是四边形
是四边形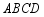 内的一点,且
内的一点,且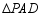 与
与 的面积相等,求
的面积相等,求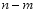 的值.
的值.
如图,已知线段 ,点 在平面直角坐标系 内.
(1)用直尺和圆规在第一象限内作出点 ,使点 到两坐标轴的距离相等,且与点 的距离等于 .(保留作图痕迹,不写作法)
(2)在(1)的条件下,若 , 点的坐标为 ,求 点的坐标.
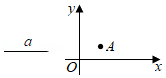
如图1,平面直角坐标系 中,等腰 的底边 在 轴上, ,顶点 在 的正半轴上, ,一动点 从 出发,以每秒1个单位的速度沿 向左运动,到达 的中点停止.另一动点 从点 出发,以相同的速度沿 向左运动,到达点 停止.已知点 、 同时出发,以 为边作正方形 ,使正方形 和 在 的同侧,设运动的时间为 秒 .
(1)当点 落在 边上时,求 的值;
(2)设正方形 与 重叠面积为 ,请问是否存在 值,使得 ?若存在,求出 值;若不存在,请说明理由;
(3)如图2,取 的中点 ,连结 ,当点 、 开始运动时,点 从点 出发,以每秒 个单位的速度沿 运动,到达点 停止运动.请问在点 的整个运动过程中,点 可能在正方形 内(含边界)吗?如果可能,求出点 在正方形 内(含边界)的时长;若不可能,请说明理由.
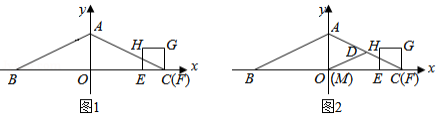
如图所示,拋物线与
轴交于
、
两点,与
轴交于点
,且点
的坐标为
,点
的坐标为
,对称轴为直线
.点
是抛物线上一个动点,设点
的横坐标为
,连接
,
,
,
.
(1)求抛物线的函数表达式;
(2)当的面积等于
的面积的
时,求
的值;
(3)在(2)的条件下,若点是
轴上一动点,点
是抛物线上一动点,试判断是否存在这样的点
,使得以点
,
,
,
为顶点的四边形是平行四边形.若存在,请直接写出点
的坐标;若不存在,请说明理由.
在平面直角坐标系中,正方形的四个顶点坐标分别为
,
,
,
.
(1)填空:正方形的面积为 ;当双曲线与正方形
有四个交点时,
的取值范围是: ;
(2)已知抛物线顶点
在边
上,与边
,
分别相交于点
,
,过点
的双曲线
与边
交于点
.
①点是平面内一动点,在抛物线
的运动过程中,点
随
运动,分别求运动过程中点
在最高位置和最低位置时的坐标;
②当点在点
下方,
,点
不与
,
两点重合时,求
的值;
③求证:抛物线与直线
的交点
始终位于
轴下方.

一个不透明的袋子中装有四个小球,上面分别标有数字,
,0,1,它们除了数字不同外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是 .
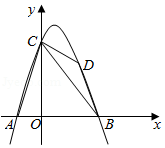
(2)小聪先从袋子中随机摸出一个小球,记下数字作为平面直角坐标系内点的横坐标;然后放回搅匀,接着小明从袋子中随机摸出一个小球,记下数字作为点
的纵坐标.如图,已知四边形
的四个顶点的坐标分别为
,
,
,
,请用画树状图或列表法,求点
落在四边形
所围成的部分内(含边界)的概率.
