在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从A地沿相同路线骑行去距A地30千米的B地,已知甲骑行的速度是乙的1.2倍.
(1)若乙先骑行2千米,甲才开始从A地出发,则甲出发半小时恰好追上乙,求甲骑行的速度;
(2)若乙先骑行20分钟,甲才开始从A地出发,则甲、乙恰好同时到达B地,求甲骑行的速度.
已知一次函数 的图象与反比例函数 的图象相交于点 , .
(1)求一次函数的表达式,并在图中画出这个一次函数的图象;
(2)根据函数图象,直接写出不等式 的解集;
(3)若点C是点B关于y轴的对称点,连接AC,BC,求△ABC的面积.

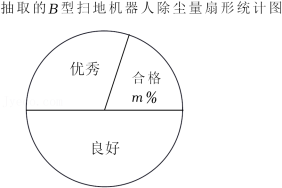
公司生产A、B两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的A、B型扫地机器人中各随机抽取10台,在完全相同条件下试验,记录下它们的除尘量的数据(单位:g),并进行整理、描述和分析(除尘量用 表示,共分为三个等级:合格 ,良好 ,优秀 ),下面给出了部分信息:
10台A型扫地机器人的除尘量:83,84,84,88,89,89,95,95,95,98.
10台B型扫地机器人中“良好”等级包含的所有数据为:85,90,90,90,94
抽取的A、B型扫地机器人除尘量统计表
|
型号 |
平均数 |
中位数 |
众数 |
方差 |
“优秀”等级所占百分比 |
|
A |
90 |
89 |
a |
26.6 |
40% |
|
B |
90 |
b |
90 |
30 |
30% |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)这个月公司可生产B型扫地机器人共3000台,估计该月B型扫地机器人“优秀”等级的台数;
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).
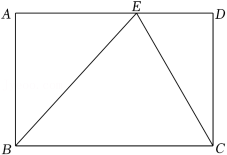
在学习矩形的过程中,小明遇到了一个问题:在矩形ABCD中,E是AD边上的一点,试说明△BCE的面积与矩形ABCD的面积之间的关系.他的思路是:首先过点E作BC的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空:
证明:用直尺和圆规,过点E作BC的垂线EF,垂足为F(只保留作图痕迹).
在△BAE和△EFB中,
∵EF⊥BC,
∴∠EFB=90°.
又∠A=90°,
∴ ①
∵AD∥BC,
∴ ②
又 ③
∴△BAE≌△EFB(AAS).
同理可得 ④
∴ .
为进一步改善生态环境,村委会决定在甲、乙、丙三座山上种植香樟和红枫.初步预算,这三座山各需两种树木数量和之比为 ,需香樟数量之比为 ,并且甲、乙两山需红枫数量之比为 .在实际购买时,香樟的价格比预算低20%,红枫的价格比预算高25%,香樟购买数量减少了6.25%,结果发现所花费用恰好与预算费用相等,则实际购买香樟的总费用与实际购买红枫的总费用之比为 .
如图,菱形ABCD中,分别以点A,C为圆心,AD,CB长为半径画弧,分别交对角线AC于点E,F.若 , ,则图中阴影部分的面积为 .(结果不取近似值)

有三张完全一样正面分别写有字母A,B,C的卡片.将其背面朝上并洗匀,从中随机抽取一张,记下卡片上的字母后放回洗匀,再从中随机抽取一张,则抽取的两张卡片上的字母相同的概率是 .
在多项式 中任意加括号,加括号后仍只有减法运算,然后按给出的运算顺序重新运算,称此为“加算操作”.例如: , ,….
下列说法:
①至少存在一种“加算操作”,使其运算结果与原多项式相等;
②不存在任何“加算操作”,使其运算结果与原多项式之和为0;
③所有可能的“加算操作”共有8种不同运算结果.
其中正确的个数是( )
| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
若关于 的一元一次不等式组 的解集为 ,且关于 的分式方程 的解是负整数,则所有满足条件的整数 的值之和是( )
| A. |
﹣26 |
B. |
﹣24 |
C. |
﹣15 |
D. |
﹣13 |
如图,AB是 的切线,B为切点,连接AO交 于点C,延长AO交 于点D,连接BD.若 ,且 ,则AB的长度是( )
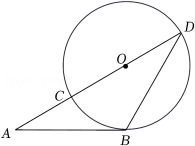
| A. |
3 |
B. |
4 |
C. |
|
D. |
|
如图,在正方形ABCD中,AE平分∠BAC交BC于点E,点F是边AB上一点,连接DF,若 ,则∠CDF的度数为( )
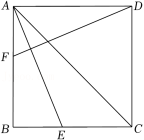
| A. |
45° |
B. |
60° |
C. |
67.5° |
D. |
77.5° |
小区新增了一家快递店,第一天揽件200件,第三天揽件242件,设该快递店揽件日平均增长率为 ,根据题意,下面所列方程正确的是( )
| A. |
|
B. |
|
| C. |
|
D. |
|