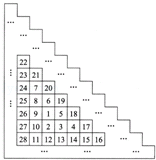
在图的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有“*”的方格内所填的数是多少?
在图的每个空格内填入一个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95。那么,标有*的格内所填的数是多少? 
请将如图所示的5×5方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,l、2、3、4、5恰好各出现一次.请问:标有符号“△”,“▽”和“○”的方格中所填的数分别是什么?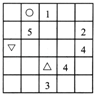
把1,2,…,9填入图20﹣1中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等.
把1,2,3,4,6,9,12,18,36这9个数分别填入3×3方格表的各方格内,使每一行、每一列及两条对角线上的3个数的乘积都是216。求位于正中间的方格中所填的数。
将从l至60的60个自然数排成一行,成为1l1位自然数,即
12345678910111213…5960.
在这111个数字中划去100个数字,余下数字的排列顺序不变,那么剩下的11位数最小可能是多少?
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
每次框出相邻的两个数,那么一共可以得到多少个不同的和?
将自然数l至9分别填在如图所示的3×3方格表内,使得每行、每列及两条对角线上的数满足两端的两个数之和减去中间的数,结果都等于5.
用l至9这9个数编制一个三阶幻方,写出所有可能的结果。所谓幻方是指在正方形的方格表的每个方格内填入不同的数,使得每行、每列和两条对角线上的各数之和相等;而阶数是指每行、每列所包含的方格的个数。
如果把1到999这些自然数按照从小到大的顺序排成一排,这样就组成了一个多位数:
12345678910111213…996997998999.
那么在这个多位数里,从左到右的第2000个数字是多少?
如图,25个同样大小的等边三角形拼成了一个大等边三角形.在每个小三角形的顶点处都标有一个数,使得任何两个相邻小等边三角形所构成的菱形的无连线的相对的顶点上所放置的数都相等.已知在大等边三角形的三个顶点放置的数分别是100、200、300.求所有顶点上数的总和.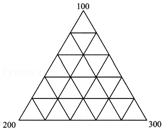
如图,把从1开始连续的自然数按照一定的顺序排成数表,如果这个数表有40行,请通过计算回答下列问题:
(1)第1行的数是多少?
(2)第20行中的最大数与最小数之和是多少?
(3)第35行中的最大数与最小数之和是多少?