如图所示,PQNM是由粗裸导线连接两个定值电阻组合成的闭合矩形导体框,水平放置,金属棒ab与PQ、MN垂直,并接触良好。整个装置放在竖直向下的匀强磁场中,磁感强度B=0.4T。已知ab长L1=0.7m,闭合矩形导体框宽L2=0.5m电阻R1=2Ω,R2=4Ω,其余电阻均忽略不计,若使ab以v=5m/s的速度向右匀速运动,求:作用于ab的外力大小及R1上消耗的电热功率(不计摩擦)
如图所示,交流发电机的电动势为E=20V,内阻不计,它通过一个R=6Ω的指示灯连接到一个理想降压变压器的输入端。在变压器的输出端并联着24只规格都是“6V,0.25W”彩色小灯泡,每只灯泡都正常发光,导线电阻不计。求:
(1)原线圈中的电流;
(2)降压变压器初级、次级线圈的匝数比;
(3)若只使用18盏彩色小灯泡,通过计算说明这时每盏小灯泡的工作状态如何?(设小灯泡的电阻不随温度变化)
内壁光滑的导热气缸竖直浸放在盛有冰水混合物的水槽中,用不计质量的活塞封闭着压强为1.0×105 Pa、体积为2.0×10-3 m3的理想气体,大气压强为1.0×105 Pa。现在活塞上方缓缓倒上沙子,使封闭气体的体积变为原来的一半,然后将气缸移出水槽,缓慢加热,使气体温度变为400 K.
(1)求气缸内气体的最终体积;
(2)在p-V图上画出缸内气体的状态变化的整个过程.
如图甲,相距为L的光滑平行金属导轨水平放置,导轨一部分处在垂直导轨平面的匀强磁场中,oo/为磁场边界,磁感应强度为B,导轨右侧接有定值电阻R,导轨电阻忽略不计。在距oo/为L处垂直导轨放置一质量为m、电阻不计的金属杆ab。
(1)若ab杆在恒力作用下由静止开始向右运动,其速度-位移的关系图象如图乙所示,则在此过程中电阻R上产生的电热Q1是多少?ab杆在离开磁场前瞬间的加速度为多少?
(2)若a b杆固定在导轨上的初始位置,磁场按Bt=Bcosωt 规律由B减小到零,在此过程中电阻R上产生的电热为Q2,求ω的大小。
在电场强度为E的匀强电场中,有一条与电场线平行的几何线,如图中虚线所示,几何线上有两个静止的小球A和B(均可看做质点),两小球的质量均为m,A球带电荷量+Q,B球不带电,开始时两球相距L,在电场力的作用下,A球开始沿直线运动,并与B球发生对碰撞,碰撞中A、B两球的总动能无损失,设在各次碰撞过程中,A、B两球间无电量转移,且不考虑重力及两球间的万有引力,问:
(1)A球经过多长时间与B球发生第一次碰撞?
(2)第一次碰撞后,A、B两球的速度各为多大?
(3)试问在以后A、B两球有再次不断地碰撞的时间吗?如果相
等,请计算该时间间隔T,如果不相等,请说明理由.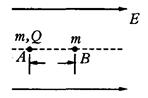
如图所示,在NOQ范围内有垂直于纸面向里的匀强磁场I,在MOQ范围内有垂直于纸面向外的匀强磁场II,M、O、N在一条直线上,∠MOQ=60°。这两个区域磁场的磁感应强度大小均为B。离子源中的离子(带电量为+q,质量为m)通过小孔O1进入极板间电压为U的加速电场区域(可认为初速度为零),离子经电场加速后通过小孔O2射出,从接近O点外进入磁场区域I。离子进入磁场的速度垂直于磁场边界MN,也垂直于磁场。不计离子的重力。
(1)当加速电场极板电压U=U0,求离子进入
磁场中做圆周运动的半径R;
(2)在OQ有一点P,P点到O点距离为L,当加速电场极板电压U取哪些值,才能保证离子通过P点。
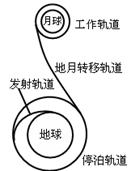
2007年10月24日18时05分“嫦娥一号”发射升空,“嫦娥一号”探月卫星的路线简化后示意图如图所示。卫星由地面发射后经过发射轨道进入停泊轨道,然后在停泊轨道经过调速后进入地---月转移轨道,再次调速后进入工作轨道,卫星开始对月球进行探测。若地球与月球的质量之比为 ,卫星的停泊轨道与工作轨道的半径之比为
,卫星的停泊轨道与工作轨道的半径之比为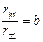 ,卫星在停泊轨道和工作轨道上均可视为做匀速圆周运动,求卫星在停泊轨道和工作轨道运行的线速度大小之比
,卫星在停泊轨道和工作轨道上均可视为做匀速圆周运动,求卫星在停泊轨道和工作轨道运行的线速度大小之比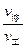 。
。
为了安全,在高速公路旁通常有安全测距警示标记,提醒司机车距必须不小于200m的安全距离,若高速公路上汽车行驶的最高速度为120km/h,某物理研究性学习小组为了弄清安全距离为200m的理论依据.查到两条相关的信息,请根据相关信息,回答以下问题。(g=10 m/s2)
资料一:驾驶员的反应时间:0.3s—0.6s之间
资料二:各种路面与轮胎之间的动摩擦因数:
| 路面 |
动摩擦因数 |
| 干沥青与混凝土路面 |
0.7—0.8 |
| 干碎石路面 |
0.6—0.7 |
| 湿沥青与混凝土路面 |
0.32—0.4 |
①在计算中驾驶员的反应时间应该取多少?为什么?
②在计算中路面与轮胎之间的动摩擦因数应该取多少?为什么?
③通过你的计算来说明200m为必要的安全距离.
如图所示,在倾角为30°的斜面OA的左侧有一竖直档板,其上有一小孔P,现有一质量m=4×10-20kg,带电量q=+2×10-14C的粒子,从小孔以速度v0=3×104m/s水平射向磁感应强度B=0.2T、方向垂直纸面向里的一正三角形区域.该粒子在运动过程中始终不碰及竖直档板,且在飞出磁场区域后能垂直打在OA面上,粒子重力不计.求: (1)粒子在磁场中做圆周运动的半径;
(1)粒子在磁场中做圆周运动的半径;
(2)粒子在磁场中运动的时间;
(3)正三角形磁场区域的最小边长.
宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部的最低点,静止一质量为m的小球(可视为质点)如图所示,当给小球水平初速度v0时,刚好能使小球在竖直面内做完整的圆周运动。已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G。若在月球表面上发射一颗环月卫星,所需最小发射速度为多大?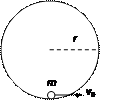
如图所示,两根不计电阻的倾斜平行导轨与水平面的夹角θ=37o ,底端接电阻R=1.5Ω.金属棒ab的质量为m=0.2kg.电阻r=0.5Ω,垂直搁在导轨上,金属棒ab与导轨间的动摩擦因数为μ=0.25,虚线为一曲线方程y=0.8sin(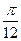 x)m与x轴所围空间区域存在着匀强磁场,磁感应强度B=0.5T,方向垂直于导轨平面向上(取g=10m/s2,sin37o=0.6,cos37o=0.8).求:
x)m与x轴所围空间区域存在着匀强磁场,磁感应强度B=0.5T,方向垂直于导轨平面向上(取g=10m/s2,sin37o=0.6,cos37o=0.8).求:
(1)当金属棒ab以速度为 m/s做匀速下滑时,电阻R的电功率是多少?
m/s做匀速下滑时,电阻R的电功率是多少?
(2)当金属棒ab从静止开始运动到Xo=6m处时,电路中的瞬时电功率为0.8w,在这一过程中,安培力对金属棒ab做了多少功?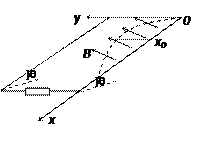
两个带电粒子的电量相同,质量之比m1∶m2=1∶4,它们以相同的初动能同时垂直于磁场方向射入到同一匀强磁场中。⑴求这两个粒子的运动半径之比、周期之比、角速度之比;⑵若质量为m1的带电粒子在磁场中转了20圈,求质量为m2的粒子在磁场中转了几圈?(粒子重力不计)
人类的陆上运输经历了从马车到蒸汽机车,再到内燃机车的演变过程。今天,我们已拥有汽车、火车、飞机等快速变通工具。
| 1. |
汽车、火车、飞机在行驶中都会因某些因素而影响其速度,所以高速运行的交通工具的头部一般呈流线型,主要是为了减少。 |
| 2. |
某汽车的部分参数如下表,请根据表中数据完成表的其他部分。
|
| 3. |
生活中经常用"呼啸而来"形容正在驶近的车辆,这是声波在传播过程中对接收者而言频率发生变化的表现,无线电波也具有这种效应。图中的测速雷达正在向一辆接近的车辆发生无线电波,并接收被车辆反射的无线电波。由于车辆的运动,接收的无线电波频率与发生时不同,利用频率差 |
| 4. |
有一个小实验:当向两片竖直放置的纸片的中间吹气时,会发现两个小纸片不但不分离,反而靠拢了。这一现象告诉我们,流体运动部分产生的压强要比它周围静止部分产生的压强小。也可以概括为流速大,压强小、流速小,压强大。飞机上天就是由于机翼上下空气流速不同造成的压力差所致。
|
| 5. |
电动车所需能量由它所携带的蓄电池供给。右图为某类电动车与汽油车性能的比较。通常车用电动机的质量是汽油机的4倍或5倍。为促进电动车的推广使用,在技相主主要应对电动车的等部件加以改进。给电动车蓄电池充电的能量实际上来自于发电站。一般发电站燃烧燃料所释放出来的能量仅30%转化为电能,在向用户输送及充电过程中又损失了20%,这意味着使用电动车时能量转化的总数率约为%。
|
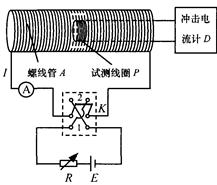
如图所示是测量通电螺线管内部磁感应强度
及其与电流
关系的实验装置。将截面积为
、匝数为
的小试测线圈
置于螺线管
中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀。将试测线圈引线的两端与冲击电流计
相连。拨动双刀双掷换向开关
,改变通入螺线管的电流方向,而不改变电流大小,在
中产生的感应电流引起
的指针偏转。
(1)将开关合到位置1,待螺线管中的电流稳定后,再将
从位置1拨到位置2,测得
的最大偏转距离为
,已知冲击电流计的磁通灵敏度为
,
=
,式中
为单匝试测线圈磁通量的变化量。则试测线圈所在处磁感应强度
=;若将
从位置1拨到位置2的过程所用的时间为
,则试测线圈
中产生的平均感应电动势
=。
(2)调节可变电阻,多次改变电流并拨动
,得到
中电流
和磁感应强度
的数据,见右表。由此可得,螺线管
内部在感应强度
和电流
的关系为
= 。
| 实验次数 |
||
| 1 |
0.5 |
0.62 |
| 2 |
1.0 |
1.25 |
| 3 |
1.5 |
1.88 |
| 4 |
2.0 |
2.51 |
| 5 |
2.5 |
3.12 |
(3)(多选题)为了减小实验误差,提高测量的准确性,可采取的措施有()
| A. |
适当增加试测线圈的匝数 |
| B. |
适当增大试测线圈的横截面积 |
| C. |
适当增大可变电阻 |
| D. |
适当拨长拨动开关的时间 |
[物理─选修3-5]
(1)天然放射性元素经过次
衰变和次
衰变,最后变成铅的同位素。(填入铅的三种同位素
、
、
中的一种)
(2)某同学利用如图所示的装置验证动量守恒定律。图中两摆摆长相同,悬挂于同一高度,两摆球均很小,质量之比为1∶2。当两摆均处于自由静止状态时,其侧面刚好接触。向右上方拉动
球使其摆线伸直并与竖直方向成45°角,然后将其由静止释放。结果观察到两摆球粘在一起摆动,且最大摆角成30°。若本实验允许的最大误差为±4%,此实验是否成功地验证了动量守恒定律?