2003年6月1日，长江三峡开始下闸蓄水，到2009年三峡工程最后完工时，水库水面将达到175m高度．为了防洪的需要，在洪水到来前，要开闸放水，把水位降至145m，如图所示．这145m～175m之间的库容称为防洪库容，它有221.5亿m3,这样就能有效地把上游的洪水拦住，大大减轻了下游的防洪压力．如果把1g食盐(NaCl)溶化在221.5m3的水中，平均每升水中含有多少Na离子？(已知NaCl的摩尔质量为M=58.5g/mol)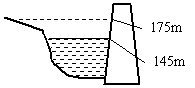
如图所示，平行金属板M、N间存在匀强电场，一质量为m电荷量为e的电子从M板附近由静止开始被电场加速，又从N板的小孔A水平射出，并垂直进入一半径为R的圆形匀强磁场区域，匀强磁场的磁感应强度为B．若入射点为C，且电子在C点的速度vC与该点所在直径OC成30o角，要使电子在磁场中通过的路程最大，则： 
(1)电子在磁场中运动的时间为多少？
(2)M、N两板间的电势差U为多少？
如图所示，同一竖直平面内固定着两水平绝缘细杆，AB＝CD＝L，两杆间竖直距离为h，BD两端与光滑绝缘的半圆形细杆相连，半圆形细杆与AB、CD在同一平面内，且AB、CD恰好为半圆弧在B、D两点处的切线，O为AD、CB连线的交点，在O点固定一电量为Q的正点电荷，质量为m的带负电小球P，电量为q，穿在细杆上．从A以一定初速度出发，沿杆滑动最后可以到达C点，已知小球与两水平杆间的动摩擦因数均为μ，小球所受库仑力始终小于重力．求：从A点出发时初速度的最小值．
如图所示是一个回旋加速器的示意图，其中两个半圆形金属盒内有方向垂直于纸面，磁感强度为B的匀强磁场，两金属盒分别接到交变电源的两极上，在两盒间的狭缝处形成交变的电场．质量为m、电量为q的带电粒子从下面盒的中心O点进入，进入时的初速可以忽略，经两盒间狭缝处的电场加速后进入上面盒内，在磁场中做圆周运动，当它回到狭缝处时，电场恰好反向，再次对粒子加速，进入下面磁场中，从c1处再进入电场中加速，以后则重复前面的过程，并且每次电场对粒子做的功都是W．图中c2、c3、……是后面各次从下面磁场中射出时的位置．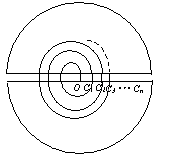
(1)求Oc1的距离．
(2)n为多大时，cncn+1小于或等于Oc1的一半？
如图所示是一种电磁泵的原理图，截面为矩形的导管PQ是运送导电液体用的，它的截面长为A．宽为b．导管的上、下两面有两块导体C．D，处于相对的位置，分别与电源的正、负极相连，通过的电流大小为I．导管的其他部分都是绝缘的．导管的通电部分位于匀强磁场中，磁场的方向与电流方向垂直，水平向右，大小为B，磁场区域的宽度为l．设液体在导管内流动时受到的阻力f的大小跟液体的流动速度v成正比，比例系数为k(即f=kv)．
(1)导管内导电液体向哪个方向流动，稳定的流动速度v0多大？
(2)已知导管内液体单位体积内的参与导电的自由电荷的数目为n、每个自由电荷的电荷量为q．求参与导电的自由电荷定向移动的平均速率．
如图所示，半径为R的光滑绝缘圆环固定在竖直平面内，在环的底端B点固定一个带正电的小球，环上还套有一个质量为m，带等量正电荷的小球，现将小球从A点(半径OA水平)由静止释放开始运动，当运动到C点(∠AOC＝
)时获得的最大动能为Ekm，求：
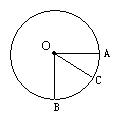
(1)小球从位置A运动到位置C的过程中所受静电力做的功W；
(2)小球在A点刚释放时运动的加速度a；
(3)小球在位置C时受到圆环对它的作用力．
足够大的平行金属板竖直放置，两板相距d，分别与直流电源的正负极相连，电源电动势E，质量为m、电量为－q的质点：沿着右板的边缘从a点开始被竖直上抛，最后在左板与a点等高的b点与左板相碰．试计算：．
(1)带点质点由a到b运动过程中，到达的最高点，相对于ab的高度多大？最高点与右板相距多远？
(2)质点与左板相碰前的瞬时速度的大小和方向．
如图所示，在高H=2.5m的光滑、绝缘水平高台边缘，静置一个小物块B，另一带电小物块A以初速度v0=10.0m/s向B运动，A．B的质量均为m=1.0×10－3kg．A与B相碰撞后，两物块立即粘在一起，并从台上飞出后落在水平地面上，落地点与高台边缘的水平距离L=5.0m．已知此空间中存在竖直向上的匀强电场，场强大小E=1.0×103N/C(图中未画出)．假设A在滑行过程和碰撞过程中电量保持不变，不计空气阻力，g=10m/s2．求：
(1)A．B碰撞过程中损失的机械能．
(2)试说明A带电的电性，并求出其电量q的大小．
(3)在A．B的飞行过程中，电场力对它做了多少功？
有些人员，如电梯修理员、牵引专家等，常需要知道绳（或金属线）中的张力T，可又不便到绳（或线）的自由端去测量．现某家公司制造了一种夹在绳上的仪表（图中B、C为该夹子的横截面）．测量时，只要如图示那样用一硬杆竖直向上作用在绳上的某点A，使绳产生一个微小偏移量a，借助仪表很容易测出这时绳对硬杆的压力F。现测得该微小偏移量为a=12 mm，BC间的距离为 2L=250mm，绳对横杆的压力为 F=300N，试求绳中的张力T.
图中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点由一不可伸长的轻绳相连，轻绳长为
．开始时，轻绳处于水平拉直状态，小球和滑块均静止．现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有粘住物质的固定挡板粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角
＝60°时小球达到最高点．求：
1.从滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量；
2.小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小．
如图所示，两绳系一质量为m=0.1kg的小球，两绳的另一端分别固定于轴的AB两处，上面绳长l=2m，两绳拉直时与轴的夹角分别为30°和45°，问球的角速度在什么范围内两绳始终有张力?
如图6-3-20是打秋千的示意图，最初人直立站在踏板上(A点所示)，绳与竖直方向成
角，人的重心到悬点O的距离为
；从A点向最低点B运动过程中，人由直立状态自然下蹲，在B点人的重心到悬点O的距离为
；在最低点处，人突然由下蹲变成直立状态(人的重心到悬点O的距离恢复为)且保持该状态到最高点C.设人的质量为m，踏板和绳的质量不计，空气阻力不计.求：
人刚到最低点B还处于下蹲状态时，两根绳中的总拉力F为多大？
人到达左端最高点C时，绳与竖直方向的夹角
为多大？(用反三角函数表示)
如图6-3-19所示，半径为R的光滑半圆上有两个小球，质量分别为m和M（M＞m），由细绳挂着，今由静止开始释放，当小球m到达半圆柱体顶端时对圆柱体的压力多大？
如图6-2-14，摩托车做腾跃特技表演，以初速
冲上高为h、顶部水平的高台，然后从高台水平飞出。若摩托车始终以额定功率P行驶，经时间t从坡底到达坡顶，人和车的总质量为m，且各种阻力的影响可忽略不计，求：
人和车到达坡顶时的速度
；人和车飞出的水平距离s；
当h为多少时，人和车飞出的水平距离最远?
.今用水平推力将其推出桌子，问怎样施力可使水平推力做的功最少？最少的功为多大？你能写出几种方案？（g取10m/s2）
粤公网安备 44130202000953号