AB两地间铺有通讯电缆,长为L,它是由两条并在一起彼此绝缘的均匀导线组成的,通常称为双线电缆。在一次事故中经检查断定是电缆上某处的绝缘保护层损坏,导致两导线之间漏电,相当于该处电缆的两导线之间接了一个电阻。检查人员经过下面的测量可以确定损坏处的位置:(1)令B端的双线断开,在A处测出双线两端间的电阻RA;(2)令A端的双线断开,在B处测出双线两端间的电阻RB;(3)在A端的双线间加一已知电压UA,在B端用内阻很大的电压表测出双线间的电压UB。
试由以上测量结果确定损坏处的位置。
某小型水电站,水以 3 m / s 的速度流入水轮机,而以 l m / s 的速度流出。流出水位比流入水位低1. 6 m ,水流量为 2 m3/s。如果水流能量的75% 供给发电机。求:
⑴ 若发电机效率为 80%,则发电机的输出功率为多大?
⑵ 发电机的输出电压为240V,输电线路的电阻为19.2Ω ,许可损耗功率为 2%,用户所需电压为220V,则所用升压变压器和降压变压器的原、副线圈匝数的比各是多少?
2006年7月1日,世界上海拔最高、线路最长的青藏铁路全线通车,青藏铁路安装的一种电磁装置可以向控制中心传输信号,以确定火车的位置和运动状态,其原理是将能产生匀强磁场的磁铁安装在火车首节车厢下面,如图甲所示(俯视图),当它经过安放在两铁轨间的线圈时,线圈便产生一个电信号传输给控制中心。线圈边长分别为 和
和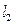 ,匝数为n,线圈和传输线的电阻忽略不计。若火车通过线圈时,控制中心接收到线圈两端的电压信号u与时间t的关系如图乙所示(ab、cd均为直线),
,匝数为n,线圈和传输线的电阻忽略不计。若火车通过线圈时,控制中心接收到线圈两端的电压信号u与时间t的关系如图乙所示(ab、cd均为直线),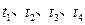 是运动过程的四个时刻,则火车( )
是运动过程的四个时刻,则火车( )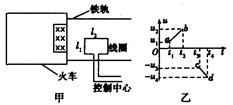
A.在 时间内做加速直线运动 时间内做加速直线运动 |
B.在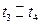 时间内做匀减速直线运动 时间内做匀减速直线运动 |
C.在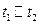 时间内加速度大小为 时间内加速度大小为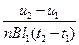 |
D.在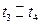 时间内平均速度的大小为 时间内平均速度的大小为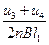 |
如图所示,匀强电场的场强方向与竖直方向成 角,一带电荷量为
角,一带电荷量为 、质量为
、质量为 的小球用细线系在竖直墙上,恰好静止在水平位置。求小球所带电荷的电性及场强的大小。
的小球用细线系在竖直墙上,恰好静止在水平位置。求小球所带电荷的电性及场强的大小。
如图所示,M、N为两平行金属板相距d="0.4" m,板间有垂直纸面的匀强磁场B="0.25" T。图中I和Ⅱ是两根与M、N平行的金属导轨,I与M相距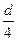 、Ⅱ与N相距
、Ⅱ与N相距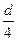 ,I与Ⅱ之间接一电阻R="0." 3Ω。现有一金属杆在上述装置上(接触良好)向右水平运动,已知金属杆ab间电阻
,I与Ⅱ之间接一电阻R="0." 3Ω。现有一金属杆在上述装置上(接触良好)向右水平运动,已知金属杆ab间电阻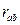 ="0." 2Ω,若有一个带电量
="0." 2Ω,若有一个带电量 C的粒子以
C的粒子以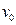 ="7" m/s沿水平向右射入MN间,恰好能匀速运动。求:
="7" m/s沿水平向右射入MN间,恰好能匀速运动。求: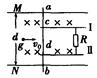
(1)两极间电势差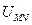 。
。
(2)ab杆运动速度。
(3)为保持ab杆匀速运动,所需外力F。
物理兴趣小组的同学发现不同的变压器,它们的初级线圈和次级线圈的匝数都不一样,于是他们提出了一个这样的探究问题:是不是变压器的输出电压与变压器的匝数有关呢?为了验证自己的猜想,他们进行了以下的探究实验:
实验器材有:可拆变压器(即初级线圈、次级线圈匝数都可改变),交流电流表,学生电源(可输出低压交流电)其实验原理图如图13-4-12所示,每次实验后每同时改变依次初级线圈、次级线圈的匝数,并将每次实验时初级线圈、次级线圈的匝数记录在表格中,同时将每次初级线圈的输入电压、次级线圈的输出电压也记录在下表中:
| 试验次数 |
初级线圈匝数n1(匝) |
次级线圈匝数n2(匝) |
n1/n2 |
初级线圈的输入电压U1(V) |
次级线圈的输出电压U2(V) |
U1/U2 |
| 1 |
1800 |
900 |
|
4 |
1.98 |
|
| 2 |
1500 |
750 |
|
4 |
1.99 |
|
| 3 |
1000 |
500 |
|
4 |
2.00 |
|
| 4 |
800 |
400 |
|
4 |
1.99 |
|
(1)计算出每次实验所用的初级线圈与次级的匝数比以及初级线圈的输入电压与次级线圈的输出电压之比并填入表中
(2)通过以上实验的数据分析,得出相应的规律:
如图所示,水平光滑平行导轨间距L=lm,左端接有阻值R=1.5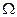 的定值电阻,在距左端
的定值电阻,在距左端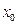 =2m处垂直导轨放置一根质量m=1kg、电阻r=0.5
=2m处垂直导轨放置一根质量m=1kg、电阻r=0.5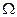 的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中。
的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中。
(1)若磁场的磁感应强度B随时间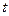 变化的关系为
变化的关系为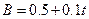 (式中B的单位为T,
(式中B的单位为T,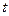 的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间
的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间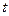 变化的规律;
变化的规律;
(2)若磁场的磁感应强度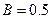 T恒定,
T恒定,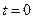 时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知
时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知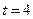 s时F=3N,求此时导体棒两端的电势差。
s时F=3N,求此时导体棒两端的电势差。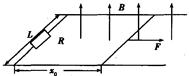
如图20所示,R1、R2为定值电阻,R3为滑动变阻器。3个电阻采用如图(a)方式接在电源上,已知R1=3Ω、R2=12Ω。现利用电压传感器(相当于电压表)和电流传感器(相当于电流表)研究R3上的电压与电流变化关系,任意滑动R3上的滑片,通过数据采集器将电压与电流信号输入计算机后,在屏幕上得到的U-I图像为如图(b)所示的一条直线(实线部分)。求:
(1)此电源的电动势、内电阻各是多少?
(2)R3的最大阻值是多少?
(3)R3消耗的最大功率是多少?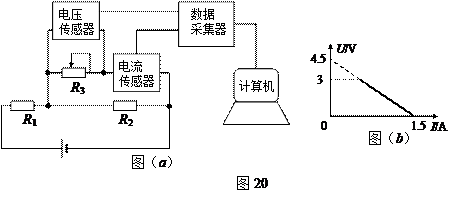
如图所示,在水平面上有两条光滑的长直平行金属导轨MN、PQ,导轨间距离为L,导轨的电阻忽略不计,磁感应强度为B的匀强磁场垂直于导轨所在平面。质量分别为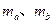 的两根金属杆a、b跨搁在导轨上,接入电路的电阻均为R。轻质弹簧的左端与b杆连接,右端被固定。开始时a杆以初速度
的两根金属杆a、b跨搁在导轨上,接入电路的电阻均为R。轻质弹簧的左端与b杆连接,右端被固定。开始时a杆以初速度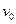 向静止的b杆运动,当a杆向右的速度为v时,b杆向右的速度达到最大值
向静止的b杆运动,当a杆向右的速度为v时,b杆向右的速度达到最大值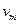 ,此过程中a杆产生的焦耳热为Q,两杆始终垂直于导轨并与导轨良好接触。求当b杆达到最大速度
,此过程中a杆产生的焦耳热为Q,两杆始终垂直于导轨并与导轨良好接触。求当b杆达到最大速度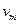 时
时
(1)b杆受到弹簧的弹力。
(2)弹簧具有的弹性势能。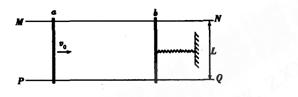
(06江苏物理卷)如图所示,顶角θ=45°,的金属导轨MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中。一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向左滑动,导体棒的质量为m,导轨与导体棒单位长度的电阻均匀为r。导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触。t=0时,导体棒位于顶角O处,求:
(1)t时刻流过导体棒的电流强度I和电流方向。
(2)导体棒作匀速直线运动时水平外力F的表达式。
(3)导体棒在0~t时间内产生的焦耳热Q。
(4)若在t0时刻将外力F撤去,导体棒最终在导轨上静止时的坐标x。
在彩色显像管中,电子从阴极通过22.5kV电势差被加速至阳极,试求电场力做的功W=?电子的电势能变化了多少?电子到达阳极时的速度v=?
如图所示,用横载面积为S的铜导线,弯成半径为r的闭合半圆形,置于磁感应强度为B的匀强磁场中,且直边与磁场方向垂直,设铜的电阻率为ρ,当半圆环以转速n绕半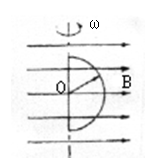 圆的直边匀速转动时,求铜半球t秒内产生的热量.
圆的直边匀速转动时,求铜半球t秒内产生的热量.
如图所示,线圈匝数n=100匝,面积S=50cm2,线圈总电阻r=10Ω,外电路总电阻R=40Ω,沿轴向匀强磁场的磁感应强度由B=0.4T在0.1s内均匀减小为零再反向增为B=0.1T,求(1)磁通量的变化率为多少?(2)感应电流大小为多少?(3)线圈的输出功率为多少?