如图10-2-11所示为一理想变压器，S为单刀双掷开关，P为滑动触头，U1为加在原线圈两端的交变电压，I1为原线圈中的电流，则（ ）
图10-2-11
| A．保持U1及P的位置不变，S由a合到b时，I1将增大 |
| B．保持U1及P的位置不变，S由b到a时，R消耗的功率减小 |
| C．保持U1不变，S合在a处，使P上滑，I1将增大 |
| D．保持P的位置不变，S合在a处，U1增大，I1将增大 |
如图13-1所示电路中的变压器为理想变压器,S为单刀双掷开关,P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I1、I2分别为原线圈和副线圈中的电流.下列说法正确的是（ ）
图13-1
| A．保持P的位置及U1不变,S由b切换到a,则R上消耗的功率减小 |
| B．保持P的位置及U1不变,S由a切换到b,则I2减小 |
| C．保持P的位置及U1不变,S由b切换到a,则I1增大 |
| D．保持U1不变，S接在b端，将P向上滑动，则I1减小 |
带电粒子（不计重力）以水平初速度v0垂直于电场方向进入水平放置的平行金属板形成的匀强电场中，它离开电场时的速度偏离原来方向的偏向角为θ，竖直偏移的距离为h，则下列说法正确的是
| A．粒子在电场中做类似平抛的运动 |
| B．偏向角θ与粒子的电荷量和质量无关 |
| C．粒子飞过电场的时间取决于极板长度和粒子进入电场时的初速度 |
| D．粒子竖直偏移的距离h可用加在两极板间的电压来控制 |
如图所示，A、B两点固定两个等量正点电荷，在A、B连线的中点C处放一点电荷（不计重力）。若给该点电荷一个初速度v0，v0方向与AB连线垂直，则该点电荷可能的运动情况是
| A．往复直线运动 |
| B．匀变速直线运动 |
| C．加速度不断减小，速度不断增大的直线运动 |
| D．加速度先增大后减小，速度不断增大的直线运动 |
如图，平行板电容器充电后与电源断开，负极板接地，在两板间有一正电荷（电荷量很小）固定在P点．以E表示两板间的场强，U表示两板间电压，W表示正电荷在P点的电势能．若负极板不动，将正极板下移到图中虚线所示的位置，则[ ]
| A．U变小，E不变 | B．E变大，W变大 |
| C．U变小，W不变 | D．E不变，W变小 |
如图所示，带正电的点电荷O固定，另有两个比荷相等的点电荷A、B分别在点电荷O的电场力作用下沿1、2两轨道运动，其中电荷A沿半径为r的圆周1以速率vA运动；电荷B沿轨道2做椭圆运动，椭圆轨道到O的最远距离为2r，电荷经过椭圆最远点时的速率是vB；两轨道相切于C点（不考虑A、B间的相互作用），则
| A．A、B两电荷均带负电 |
| B． vA等于vB |
| C．两电荷分别经过C点时速度大小相等 |
D． A电荷运动的加速度为 。 |
如图所示，理想变压器的原线圈匝数为 n1=1000匝，副线圈匝数 n2=200匝，交变电源的电动势e ="311sin314t" V，电阻R=88Ω，电流表和电压表对电路的影响忽略不计，下列结论正确的是（ AB ）
| A．电流频率为50HZ |
| B．电流表A1的示数约为0.1A |
| C．电压表V1的示数为311V |
| D．电阻R的发热功率约为44W |
用比值法定义物理量是物理学中一种常用的方法．下面四个物理量都是用比值法定义的，其中定义式正确的是（ ）
A．电容C= |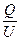
B．磁感应强度B= |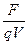
C．电场强度E= |
D．电阻R= |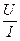
在绕制变压器时，某人误将两个线圈绕在如图所示变压器铁心的左右两个臂上，当通以交变电流时，每个线圈产生的磁通量都只有一半通过另一个线圈，另一半通过中间的臂，已知线圈1、2的匝数之比N1：N2=2：1，在不接负载的情况下（ ）
| A．当线圈1输入电压220V时，线圈2输出电压为110V |
| B．当线圈1输入电压220V时，线圈2输出电压为55V |
| C．当线圈2输入电压110V时，线圈1输出电压为220V |
| D．当线圈2输入电压110V时，线圈1输出电压为110V |
如图,为一理想变压器,K为单刀双掷开关,P为滑动变阻器的滑动触头, 
为加在原线圈两端的电压, 
为原线圈中的电流强度,则:
A，保持及P的位置不变,K由a合到b时, 将增大
B，保持及P的位置不变,K由b合到a时,R消耗的功率减小
C，保持不变,K合在a处,使P上滑, 将增大
D，保持P的位置不变,K合在a处,若增大,将增大
如图所示，自耦变压器输入端、
接交流稳压电源，其电压有效值
，
，当滑动片处于线圈中点位置时，
、
两端电压的有效值
为
，通过电阻
的电流有效值为
．
粤公网安备 44130202000953号
