一个单摆在质量为m1、半径为R1的星球上做周期为T1的简谐运动，在质量为m2、半径为R2的星球上做周期为T2的简谐运动。求T1与T2之比。
两架单摆,它们的摆长之比为l1：l2=4：1,摆球质量之比m1：m2=2：1,摆动中它们的摆角相同,摆球通过最低点时的动能之比Ek1：Ek2=
| A．2：1 | B．4：1 | C．8：1 | D．16：1 |
如下图中，摆球A、B用细线悬挂在天花板上，两球刚好接触，现将摆球A在两摆线所在平面内向左拉开一小角度后释放，碰撞后，两摆球分开各自做简谐运动，以mA、mB分别表示A、B摆球的质量，则( )
A、如果mA＞mB，下一次碰撞将发生在平衡位置右侧
B、如果mA＜mB，下一次碰撞将发生在平衡位置左侧
C、无论两摆球的质量之比是多少，下一次碰撞都不可能在平衡位置右侧
D、无论两摆球的质量之比是多少，下一次碰撞都不可能在平衡位置左侧
把地球上的一个秒摆(周期等于2s的摆称为秒摆)拿到月球上去，它的振动周期变为多少？已知：地球质量M地=5.98×1024kg，半径R地=6.4×106m，月球质量M月=7.34×1022kg，半径R月=1.74×106m。
如图所示，若单摆处于沿水平方向作匀加速直线运动的系统内，单摆的摆长为L，系统水平向右的加速度为a，摆球的质量为m，求这一单摆的周期。
如图所示，将单摆小球A从静止释放的同时，高出悬点O的另一小球B做自由落体运动，结果它们同时到达跟单摆的平衡位置C等高处．已知摆长为l，偏角θ＜5°，求：B球的初位置与单摆悬点之间的高度差h．
如图，两个完全相同的弹性小球A和B分别悬挂在两根长度分别为L和4L的不可伸长的轻绳末端，两绳均处于竖直状态，两小球重心在同一水平线上且刚好相互接触，现将A球拉到一个很小的角度由静止释放，则在A球运动的2个周期内，两球相碰的次数为
| A．1次 | B．2次 | C．3次 | D．4次 |
在地质、地震、勘探、气象和地球物体等领域的研究中，需要精密的重力加速度g值，g值可由实验精确测定。近年来测g值的一种方法叫“对称自由下落法”，它是将测g值归于测长度和时间，以稳定的氦氖激光的波长为长度标准，用光学干涉的方法测距离，以铷原子钟或其他手段测时间，能将z值测得很准。具体做法是：将真空长直管沿竖直方向放置，在其中O点向上抛小球，小球从抛出到落回原处的时间为T2，在小球上升过程中经过比O点高H的P点，小球离开P点至又回到P点所用的时间为T1，测得T1、T2和H，可求得g等于 （ ）
A． |
B． |
C． |
D． |
图8所示，用两根长度都为1的细线悬挂一个小球A，绳子与水夹角为α，使A球垂直于纸面作摆角小于5度的摆动，当它经过平衡位置的瞬间，有另一个小球B，从A球的正上方的H高处自由落下，并击中A球，则最初B球队距A球的高度H可能是：
| A．0.5π2lsinα | B．2π2lsinα | C．3π2lsinα | D．8π2lsinα |
质量相同的两个小球，分别用长为l和2 l的细绳悬挂在天花板上，如图所示，分别拉起小球使线伸直呈水平状态，然后轻轻释放，当小球到达最低位置时 
| A．两球运动的线速度相等 |
| B．两球运动的角速度相等 |
| C．两球运动的加速度相等 |
| D．细绳对两球的拉力相等 |
如图5所示为同一地点的两单摆甲、乙的振动图象，下列说法中正确的是（ ）
| A．甲、乙两单摆的摆长相等 | B．甲摆的振幅比乙摆大 |
| C．甲摆的机械能比乙摆大 | D．在t＝0.5 s时有正向最大加速度的是乙摆 |
关于单摆下列说法正确的是 ( )
| A．摆球运动的回复力是摆线张力和重力的合力 |
| B．摆球经过轨迹上的同一点速度是相同的 |
| C．摆球经过轨迹上的同一点加速度是相同的 |
| D．摆球经过平衡位置受力是平衡的 |
在《用单摆测定重力加速度》的实验中：
（1）某同学用秒表测得单摆完成40次全振动的时间如图(a)所示，则单摆的周期为 s。
（2）实验中对提高测量结果精度有利的建议是______。
| A．单摆的摆线不能太短 |
| B．单摆的摆球密度尽可能大 |
| C．单摆的摆角越大越好 |
| D．从平衡位置开始计时，测量一次全振动的时间作为摆动周期 |
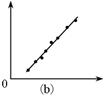
（3）若单摆在任意摆角θ时的周期公式可近似为T=T0[1+asin2(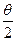
)]，式中T0为摆角趋近于0°时的周期，a为常数；为了用图象法验证该关系式，需要测量的物理量有________；某同学在实验中得到了如图(b)所示的图线，则图线的斜率表示_______。
粤公网安备 44130202000953号