高中物理探究单摆的周期与摆长的关系填空题

一个单摆在甲地时，在时间t内完成m次全振动，移至乙地时，经过相同的时间完成n次全振动，则甲、乙两地重力加速度大小之比g_甲：g_乙等于______________。

如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球

某同学在用单摆测定重力加速度的实验中，测量不同摆长情况下单摆的振动周期，并以L为横坐标，为纵坐标，做出了图线，如图所示，由此图线可知重力加速度为            m/s²。　　　　　　　　　　　　　　　　　　　

有两个单摆做简谐运动，位移与时间关系是：x₁=3asin(4πbt+)和x₂=9asin(8πbt+)，其中a、b为正的常数，则它们的：振幅之比为__________；摆长之比为_________。

如图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置。设摆球向右运动为正方向。图乙是这个单摆的振动图象。(取g＝10 m/s²)

(1)由图象可知，单摆振动的频率为____     ____Hz。
(2)t＝0时，摆球应在___      _____点。
(3)此摆的摆长为___       _____m。

如图所示为一单摆的共振曲线，根据曲线可求得此单摆摆长为       ，若该单摆的摆长变短，则此共振曲线振幅A最大值对应的横坐标f的值将      （选填“增大”、“减小”或“不变”）（取g=π²）。

两个摆长相同的单摆，摆球质量之比是4:1，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为             。

如图，蛇形摆是演示单摆周期与摆长关系的实验装置。现将10个摆球由平衡位置沿x轴正方向移动相同的一小位移，然后同时释放，摆球整体看上去像舞动的蛇。从左向右，10个摆的振动周期依次       (选填“增大”、“减小”或“不变”)；若摆长最长的摆为秒摆(周期为2s)，则其摆长为     m(取g＝9.80m/s²，结果保留1位有效数字)。

如右图甲所示，有一质量为m、带电量为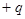的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为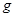，则周期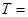        ；若在悬点处放一带正电的小球（图乙），则周期将        。（填“变大”、“不变”、“变小”）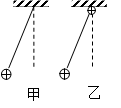

有两个同学分别在大庆和广州的物理实验室，各自在那里利用先进的DIS系统较准确地探究了“单摆的周期T与摆长l的关系”，他们通过互联网交换实验数据，并由计算机绘制了T²－l图像，如图甲所示．在大庆的同学所测实验结果对应的图线是________(填“A”或“B”)．另外，在广州做探究的同学还利用计算机绘制了a、b两个摆球的振动图像(如图乙)，由图可知，两单摆摆长之比＝________.在t＝1 s时，b球振动的方向是________．

甲　　　　　　　　　          乙

在“用单摆测定重力加速度”的某次实验中，摆长为L的单摆完成n次全振动的时间为t，则单摆的周期为　　，重力加速度大小为　　

如图所示的单摆，摆球a向右摆动到最低点时，恰好与一沿水平方向向左运动的粘性小球b发生碰撞，并粘接在一起，且摆动平面不变。已知碰撞前a球摆动的最高点与最低点的高度差为h，偏角θ较小，摆动的周期为T，a球质量是b球质量的4倍，碰撞前a球在最低点的速度是b球速度的一半。则碰撞后，摆动的周期为_________T，摆球的最高点与最低点的高度差为_________ h。

一个单摆的振动周期为T。若只将摆长缩为原来的时，周期为      ；若只将摆球质量减为原来的时，周期为      ；若只将振幅减为原来的时，周期为       。

如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球

如图，在半径为的光滑圆环上切下一小段圆弧，放置于竖直平面内，两端点距最低点高度差为。将小环置于圆弧端点并从静止释放，小环运动到最低点所需的最短时间为，在最低点处的加速度为。(取)