如图所示,两段光滑圆弧轨道半径分别为R1和R2,圆心分别为O1和O2,所对应的圆心角均小于5°,在最低点O平滑连接。M点和N点分别位于O点左右两侧,距离MO小于NO。现分别将位于M点和N点的两个小球A和B(均可视为质点)同时由静止释放。关于两小球第一次相遇点的位置,下列判断正确的是
| A.恰好在O点 | B.一定在O点的左侧 |
| C.一定在O点的右侧 | D.条件不足,无法确定 |
下列关于单摆周期的说法正确的是( )
| A.用一个装满砂的漏斗和长细线做成一个单摆,在摆动时砂从漏斗中缓慢漏出,周期不变 |
| B.当升降机向上匀加速运动时(a<g)单摆的周期小于电梯匀速运动时单摆的周期 |
| C.将摆由赤道移到北极,单摆振动周期减小 |
| D.将单摆的摆角由5°增加到10°(不计空气阻力),单摆的周期减小 |
如图所示,曲面AO是一段半径为2m的光滑圆弧面,圆弧与水平面相切于O点,AO弧长10cm.现将一小球先后从曲面的顶端A和AO弧的中点B由静止释放,到达底端O的速度分别为v1和v2,所经历的时间分别是t1和t2,那么( )
| A.v1>v2,t1>t2 |
| B.v1=v2, t1>t2 |
| C.v1>v2,t1=t2 |
| D.v1=v2, t1=t2 |
如图所示,A、B分别为单摆做简谐振动时摆球的不同位置.其中,位置A为摆球摆动的最高位置,虚线为过悬点的竖直线.以摆球最低位置为重力势能零点,则摆球在摆动过程中
A、位于B处时动能最大
B、位于A处时势能最大
C、在位置A的势能大于在位置B的动能
D、在位置B的机械能大于在位置A的机械能
如图所示,将小球甲、乙、丙(都可视为质点)分别从A、B、C三点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从圆心A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D,丙沿圆弧轨道从C点运动D,且C点很靠近D点。如果忽略一切摩擦阻力,那么下列判断正确的是:( ) 
A.甲球最先到达D点,乙球最后到达D点
B.甲球最先到达D点,丙球最后到达D点
C.丙球最先到达D点,乙球最后到达D点
D.甲球最先到达D点,无法判断哪个球最后到达D点
摆长为L的单摆做简谐运动,若从某时刻开始计时(取t=0),当振动至t= 时,摆球具有负向最大速度,则单摆的振动图象是图中的 ( )
时,摆球具有负向最大速度,则单摆的振动图象是图中的 ( )
一单摆的摆长为40cm,摆球在t=0时刻正从平衡位置向右运动,若g取10 m/s2,则在1s时摆球的运动情况是 :
| A.正向左做减速运动,加速度正在增大 | B.正向左做加速运动,加速度正在减小 |
| C.正向右做减速运动,加速度正在增大 | D.正向右做加速运动,加速度正在减小 |
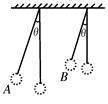
如图所示,两个单摆A和B,其摆长LA>LB,将它们都拉离竖直方向一个很小的角度 ,然后由静止释放,那么两个球到达最低点时的速度大小与经历时间关系的多少为()
,然后由静止释放,那么两个球到达最低点时的速度大小与经历时间关系的多少为() 
| A.vA>vB,tA>tB | B.vA<vB,tA<tB |
| C.vA>vB,tA<tB | D.vA<vB,tA>tB |
单摆做简谐运动的回复力是( )
| A.摆球的重力 |
| B.摆球所受重力与悬线对摆球的拉力的合力 |
| C.悬线对摆球的拉力 |
| D.摆球所受重力在圆弧切线方向上的分力 |
如图所示,单摆摆球的质量为m,做简谐运动的周期为T,摆球从最大位移A处由静止释放,摆球运动到最低点B时的速度大小为v,不计空气阻力,则( )
A.摆球从A运动到B的过程中,重力做的功为 mv2 mv2 |
B.摆球从A运动到B的过程中,重力做的功的平均功率为 |
| C.摆球运动到B时重力的瞬时功率为mgv |
| D.摆球从A运动到B的过程中合力的冲量大小为mv |
如图所示,单摆的摆线是绝缘的,摆长为L,摆球带正电,摆悬挂于O点,在AD间摆动,当它摆过竖直线OC时便进入磁感应强度为B的有界匀强磁场,磁场方向垂直于单摆的摆动平面向里,下列说法正确的是( )
| A.A与D处于同一水平面 |
B.单摆的周期T=2π |
C.单摆的振动周期T>2π |
| D.单摆向右或向左摆过同一点C时摆线的张力一样大 |
如图所示,一单摆悬于O点,摆长为L,若在O点的竖直线上的O′点钉一个钉子,使OO′=L/2,将单摆拉至A处释放,小球将在A、B、C间来回振动,若振动中摆线与竖直方向夹角小于10°,则此摆的周期是( )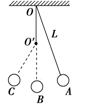
A.2π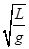 B.2π
B.2π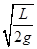
C.2π(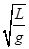 +
+ 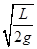 ) D.π(
) D.π(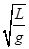 +
+ 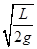 )
)
做简谐振动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减小为原来的1/2,则单摆振动的( )
| A.频率、振幅都不变 | B.频率、振幅都改变 |
| C.频率不变,振幅改变 | D.频率改变,振幅不变 |