高中物理探究单摆的周期与摆长的关系试题

由长度依次为L和2L的AC和BC两根细绳悬挂着小球G，如图所示，每根细绳跟竖直方向的夹角均为30°。当该小球向纸外做微小摆动时，其摆动周期为多少？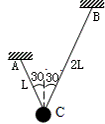

已知在单摆a完成10次全振动的时间内，单摆b完成6次振动，两摆长之差为1.6m，则两单摆摆长l_a与l_b分别为

A．la=2.5m，lb="0.9m"

B．la=0.9m，lb=2.5m

C．la=2.4m，lb="4.0m"

D．la=4.0m，lb=2.4m

如图4所示，摆长为L的单摆，小球质量为m，带正电荷，电荷量为 q，处在水平向右的场强为E的匀强电场中，现将小球拉离平衡位置（＜10°）由静止释放，求其周期。

关于振动和波动，下列说法正确的是（     ）

A．单摆做简谐运动的周期与摆球的质量有关

B．部队过桥不能齐步走而要便步走，是为了避免桥梁发生共振现象

C．在波的干涉中，振动加强的点位移不一定始终最大

D．各种波均会发生偏振现象

如图2所示，将摆长为L的单摆放在一升降机中，若升降机以加速度a向上运加速运动，求单摆的摆动周期。

下列关于单摆运动过程中的受力说法，正确的是

A．单摆运动的回复力是重力和摆线拉力的合力

B．单摆运动的回复力是重力沿圆弧切线方向的一个分力

C．单摆过平衡位置时，所受的合力为零

D．单摆运动的回复力是摆线拉力的一个分力

例如，在图中，三条长度均为L的绳子共同系住一个密度均匀的小球m，球直径为d。若摆球在纸面内做小角度的左右摆动，摆动圆弧的圆心在O1处，故等效摆长为

一单摆做小角度摆动，其振动图象如图，以下说法正确的是

A．t1时刻摆球速度最大，悬线对它的拉力最小

B．t2时刻摆球速度最大，振动方向沿x正方向

C．t3时刻摆球速度为零，加速度最大，方向沿x负方向

D．t4时刻摆球速度最大，悬线对它的拉力最大

如图所示，摆球的质量为m，半径为r，带正电荷，用长为L的细线把摆球吊在悬点O处做成单摆，在悬点O处固定着另一个正点电荷，则这个单摆的周期为（）

A．

B．

C．大于

D．小于

下列情况下，会使单摆周期变大的是

A．减少单摆摆球的质量

B．增大单摆摆球的质量

C．将摆从赤道移到北极

D．将摆从地球移到月球上

在地球表面上周期准确的秒摆（周期为2秒），移到距离地面为nR₀的高度处（R₀为地球半径），该秒摆的周期    秒，此时为了让秒摆保持周期2秒不变，则需要    (“增长”，“减短”）摆长．

用20分度的游标卡尺测量物件长度如图，由图可知其长度为          mm；

甲、乙两个单摆摆长相同，摆球质量之比为4：1．两个单摆在同一地点做简谐运动，摆球经过平衡位置时的速率之比为1：2，则两摆   

A．振幅相同，频率相同	B．振幅不同，频率相同
C．振幅相同，频率不同	D．振幅不同，频率不同

某实验小组拟用如图1所示装置研究滑块的运动。实验器材有滑块、钩码、纸带、米尺、带滑轮的木板，以及由漏斗和细线组成的单摆等。实验中，滑块在钩码作用下拖动纸带做匀加速直线运动，同时单摆在垂直于纸带运动方向摆动，漏斗漏出的有色液体在纸带上留下的痕迹记录了漏斗在不同时刻的位置。

①在图2中，从       纸带可看出滑块的加速度和速度方向一致。
②用该方法测量滑块加速度的误差主要来源有：         、
                （写出2个即可）。  

A、 B两个单摆，在同一地点A全振动10次的时间内， B恰好全振动了25次，则A、B的摆长之比为