高中物理探究单摆的周期与摆长的关系试题

在地球表面上周期准确的秒摆（周期为2秒），移到距离地面为nR₀的高度处（R₀为地球半径），该秒摆的周期    秒，此时为了让秒摆保持周期2秒不变，则需要    (“增长”，“减短”）摆长．

将一单摆向右拉至水平标志线上，从静止释放，当摆球运动到最低点时，摆线碰到障碍物，摆球继续向左摆动，用频闪照相机拍到如图所示的单摆运动过程的频闪照片，摆球从最高点M摆至左边最高点N时，以下说法正确的是（   ）

A．摆线碰到障碍物前后的摆长之比为

B．摆线碰到障碍物前后的摆长之比为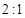

C．摆线经过最低点时，线速度不变，半径减小，摆线张力变大

D．摆线经过最低点时，角速度不变，半径减小，摆线张力变大

用20分度的游标卡尺测量物件长度如图，由图可知其长度为          mm；

关于振动和波动，下列说法正确的是（     ）

A．单摆做简谐运动的周期与摆球的质量有关

B．部队过桥不能齐步走而要便步走，是为了避免桥梁发生共振现象

C．在波的干涉中，振动加强的点位移不一定始终最大

D．各种波均会发生偏振现象

一质点做简谐运动，先后以相同的速度依次通过A、B两点，历时1s，质点通过B点后再经过1s又第2次通过B点，在这两秒钟内，质点通过的总路程为12cm，则质点的振动周期和振幅分别为（　　）
A．3s，6cm       B．4s，6cm       C．4s，9cm       D．2s，8cm

一小球挂于O点，细线长为L，O点正下方L/2处有一铁钉。将小球拉至A处无初速释放，摆角很小，这个摆的周期是：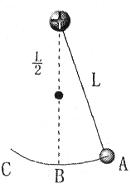

A．

B．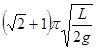

C．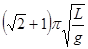

D．

甲、乙两个单摆摆长相同，摆球质量之比为4：1．两个单摆在同一地点做简谐运动，摆球经过平衡位置时的速率之比为1：2，则两摆   

A．振幅相同，频率相同	B．振幅不同，频率相同
C．振幅相同，频率不同	D．振幅不同，频率不同

甲、乙两个单摆摆长相同，摆球质量之比为4∶1，两个单摆在同一地点做简谐振动，摆球经过平衡位置时的速率之比为1∶2，则两摆 （       ）

A．振幅相同，频率相同	B．振幅不同，频率相同
C．振幅相同，频率不同	D．振幅不同，频率不同

在做《用单摆测定重力加速度》的实验时，用摆长l和周期T计算重力加速度的公式是g=           。

一单摆做小角度摆动，其振动图象如图，以下说法正确的是

A．t1时刻摆球速度最大，悬线对它的拉力最小

B．t2时刻摆球速度最大，振动方向沿x正方向

C．t3时刻摆球速度为零，加速度最大，方向沿x负方向

D．t4时刻摆球速度最大，悬线对它的拉力最大

做简谐振动的单摆，在摆动的过程中(　　)

A．只有在平衡位置时，回复力才等于重力和细绳拉力的合力

B．只有在最高点时，回复力才等于重力和细绳拉力的合力

C．小球在任意位置处，回复力都等于重力和细绳拉力的合力

D．小球在任意位置处，回复力都不等于重力和细绳拉力的合力

对单摆的振动，以下说法中正确的是（   ）

A．单摆摆动时，摆球受到的向心力大小处处相等

B．摆球经过平衡位置时所受合外力为零

C．摆球经过平衡位置时所受回复力为零

D．单摆运动的回复力是摆球所受合力

一座在地球上走时准确的摆钟，到某行星上后，分针走一圈经历的实际时间是3小时，已知该行星的半径是地球半径的1/4，则该行星上的第一宇宙速度应为地球上的第一宇宙速度的（    ）

A．2/3

B．3/2

C．1/6

D．6

有一个单摆, 当摆线与竖直方向成θ角(θ<5°)时, 摆球的速度为零。已知当地的重力加速度为g，摆球运动到最低点时速度为V,则单摆的振动周期为           。

某实验小组拟用如图1所示装置研究滑块的运动。实验器材有滑块、钩码、纸带、米尺、带滑轮的木板，以及由漏斗和细线组成的单摆等。实验中，滑块在钩码作用下拖动纸带做匀加速直线运动，同时单摆在垂直于纸带运动方向摆动，漏斗漏出的有色液体在纸带上留下的痕迹记录了漏斗在不同时刻的位置。

①在图2中，从       纸带可看出滑块的加速度和速度方向一致。
②用该方法测量滑块加速度的误差主要来源有：         、
                （写出2个即可）。