高中物理探究弹力和弹簧伸长的关系计算题

如图所示，质量为0.7kg的物体A放在倾角为37°的斜面上，未施加其他力时物体恰好沿斜面匀速下滑。
（已知重力加速度g =10m/s² ,sin37⁰="0.6" ,cos37⁰=0.8）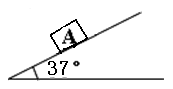

（1）求物体与斜面间的动摩擦因数
（2）若对A施加一个水平向右的推力，刚好可使A物体沿斜面向上做匀速直线运动，求水平推力力为多大？

如图，原长分别为L_1­和L₂，劲度系数分别为k₁和k₂的轻质弹簧竖直地悬挂在天花板上，两弹簧之间有一质量为m₁的物体，最下端挂着质量为m₂的另一物体，整个装置处于静止状态。现用一个质量为m的平板把下面的物体竖直地缓慢地向上托起，直到两个弹簧的总长度等于两弹簧原长之和。求：

（1）这时托起平板竖直向上的力是多少？
（2）整个过程m₂上升的高度是多少？

如图所示，重力为G₁=8N的砝码悬挂在绳PA和PB的结点上，PA偏离竖直方向37°角，PB沿水平方向且连在重力为G₂=10N的木块上，木块静止于倾角为37°的斜面上，试求：

（1）木块与斜面间的摩擦力；
（2）木块所受斜面的弹力．

如图，滑雪运动员由静止开始经过一段1/4圆弧形滑道滑行后，从弧形滑道的最低点O点水平飞出，经过3s时间落到斜坡上的A点．已知O点是斜坡的起点，斜坡与水平面的夹角θ=37°，运动员与滑雪板的总质量巩=50kg．不计空气阻力，求：（已知sin37°=0.60，cos37°=0.80，g取10m/s²，忽略弧形滑道的摩擦）

（1）在O点时滑雪板对滑道的压力大小；
（2）运动员经过O点时的速度大小．

如图甲所示，光滑的水平地面上固定一长L=1.7m的木板C，C板的左端有两个可视为质点的物块A和B，其间夹有一根原长为1.0m、劲度系数k=200N/m的轻弹簧，此时弹簧没有发生形变，且与物块不相连。已知m_A= m_C=20kg，m_B=40kg，A与木板C、B与木板C的动摩擦因数分别为μA=0.50，μB=0.25。假设最大静摩擦力与滑动摩擦力相等。现用水平力F作用于A，让F从零逐渐增大，使A缓慢移动而逐渐压缩弹簧，压缩了一定量后又推动B缓慢地向右移动，当B缓慢向右移动0.5m时，使弹簧储存了弹性势能E₀。（g=10m/s²）问：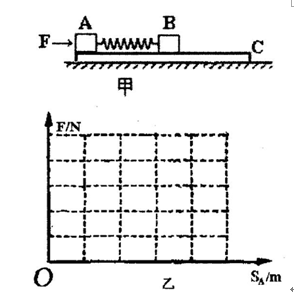

（1）以作用力F为纵坐标，物块A移动的距离为横坐标，试通过定量计算在图乙的坐标系中画出推力F随物块A位移的变化图线。
（2）求出弹簧贮存的弹性势能E₀的大小。
（3）当物块B缓慢地向右移动了0.5m后，保持A、B两物块间距，将其间夹有的弹簧更换，使得压缩量仍相同的新弹簧贮存的弹性势能为12E₀，之后同时释放三物体A、B和C，已被压缩的轻弹簧将A、B向两边弹开，设弹开时A、B两物体的速度之比始终为2：1，求哪一物块先被弹出木板C？最终C的速度是多大？

如图所示，光滑水平面上放置质量均为M＝2 kg的甲、乙两辆小车，两车之间通过一感应开关相连(当滑块滑过感应开关时，两车自动分离)．甲车上表面光滑，乙车上表面与滑块P之间的动摩擦因数μ＝0.5.一根通过细线拴着(细线未画出)且被压缩的轻质弹簧固定在甲车的左端，质量为m＝1 kg的滑块P(可视为质点)与弹簧的右端接触但不相连，此时弹簧的弹性势能E₀＝10 J，弹簧原长小于甲车长度，整个系统处于静止状态．现剪断细线，求：

①滑块P滑上乙车前的瞬时速度的大小．
②滑块P滑上乙车后最终未滑离乙车，滑块P在乙车上滑行的距离．(取g＝10 m/s²)

轻弹簧AB长35cm，A端固定在重50N的物体上，该物体放在倾角为30⁰的斜面上，如图所示，手执B端，使弹簧与斜面平行，当弹簧和物体沿斜面匀速下滑时，弹簧长变为40cm；当弹簧和物体沿斜面匀速上滑时，弹簧长度变为50cm，试求：

（1）求弹簧的劲度系数k；
（2）物体与斜面间的动摩擦因数μ．

如图所示,半径为R、质量为M的均匀球靠竖直墙放置,左下方有一厚为h、质量为m的木块。若不计摩擦,用至少多大的水平力F推木块才能使球离开地面?此时木块对地的压力为多大?

如图所示，在一根不可伸长的细线上系一个质量为m的小球，当把小球拉到使细线与水平面成θ=30°角时，轻轻释放小球．不计空气阻力，求小球刚开始做圆周运动的瞬间对细线的拉力．

如图所示，两物块A、B置于光滑水平面上，质量分别为m和2m，一轻质弹簧两端分别固定在两物块上，开始时弹簧处于拉伸状态，用手固定两物块。现在先释放物块B，当物块B的速度大小为3v时，再释放物块A，此时弹簧仍处于拉伸状态；当物块A的速度大小为v时，弹簧刚好恢复原长。自始至终弹簧都未超出弹性限度。求：

①弹簧刚恢复原长时，物块B的速度大小；
②两物块相距最近时，弹簧的弹性势能大小(设弹簧处于原长时弹性势能为零)。

如图所示，一质量为m、长为L的木板A静止在光滑水平面上，其左侧固定一劲度系数为k的水平轻质弹簧，弹簧原长为l₀，右侧用一不可伸长的轻质细绳连接于竖直墙上。现使一可视为质点小物块B以初速度v₀从木板的右端无摩擦地向左滑动，而后压缩弹簧。设B的质量为λm，当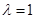时细绳恰好被拉断。已知弹簧弹性势能的表达式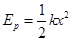，其中k为劲度系数，x为弹簧的压缩量。求：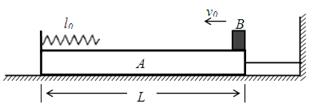

（1）细绳所能承受的最大拉力的大小F_m
（2）当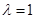时，小物块B滑离木板A时木板运动位移的大小s_A
（3）当λ＝2时，求细绳被拉断后长木板的最大加速度a_m的大小
（4）为保证小物块在运动过程中速度方向不发生变化，λ应满足的条件

如图甲所示，在倾角为37⁰的粗糙斜面的底端，一质量m=1kg可视为质点的滑块压缩一轻弹簧并锁定，滑块与弹簧不相连。t=0时解除锁定，计算机通过传感器描绘出滑块的速度时间图象如图乙所示，其中bc段为直线，g取10m/s²。求：

（1）动摩擦因数μ的大小；
（2）t=0.4s时滑块的速度v的大小。

(9分)一质量为的子弹以某一初速度水平射入置于光滑水平面上的木块并留在其中，与木块用一根弹性良好的轻质弹簧连在一起，开始弹簧处于原长，如图所示。已知弹簧被压缩瞬间的速度，木块、的质量均为。求：

子弹射入木块时的速度；
‚弹簧被压缩到最短时弹簧的弹性势能。

如图，一长为10cm的金属棒用两个完全相同的弹簧水平地悬挂在匀强磁场中；磁场的磁感应强度大小为0.1T，方向垂直于纸面向里；弹簧上端固定，下端与金属棒绝缘，金属棒通过开关与一电动势为12V的电池相连，电路总电阻为2。已知开关断开时两弹簧的伸长量均为0.5cm；闭合开关，系统重新平衡后，两弹簧的伸长量与开关断开时相比均改变了0.3cm，重力加速度大小取。判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量。

如图所示，弹簧的一端固定，另一端连接一个物块，弹簧质量不计，物块（可视为质点）的质量为，在水平桌面上沿轴转动，与桌面间的动摩擦因数为，以弹簧原长时物块的位置为坐标原点，当弹簧的伸长量为x时，物块所受弹簧弹力大小为，为常量。

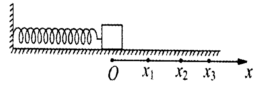
（1）请画出随变化的示意图:并根据图像，求物块沿轴从点运动到位置过程中弹力所做的功。
（2）物块由向右运动到，然后由返回到，在这个过程中。

A.求弹力所做的功；并据此求弹性势能的变化量；
B.求滑动摩擦力所做的功；并与弹力做功比较，说明为什么不存在与摩擦力对应的"摩擦力势能"的概念。