高中物理法拉第电磁感应定律试题

关于电磁感应和感应电动势，下列说法中正确的是

A．只要电路中有磁感线通过，电路中就有感应电动势产生

B．穿过电路的磁通量变化率越大，电路中的感应电动势就越大

C．穿过电路中的磁通量变化越大，电路中的感应电动势就越大

D．单位时间内穿过电路中的磁通量变化量越大，电路中的感应电动势就越大

如图所示，线圈为100匝，在2s内穿过线圈的磁通量由0.04Wb均匀增大到0.08Wb，这2s时间内线圈产生的感应电动势为       V，如果线圈回路的总电阻为1Ω，则感应电流是        A

下列各种情况中的导体切割磁感线产生的感应电动势最大的是（   ）

某地的地磁场磁感应强度的竖直分量方向向下，大小为4．5×10^－5T．一灵敏电压表连接在当地入海河段的两岸，河宽100m，该河段涨潮和落潮时有海水(视为导体)流过．设落潮时，海水自西向东流，流速为2m/s．下列说法正确的是  (　   )

A．电压表记录的电压为5 mV

B．电压表记录的电压为9 mV

C．河南岸的电势较高

D．河北岸的电势较高

关于电磁感应，下列说法不正确的有(     )
A. 闭合回路中的磁通量变化时就有感应电流，停止变化感应电流就消失
B. 之所以会有感应电流是由于电路中产生了感应电动势，所以没有感应电流就说明没有感应电动势
C. 导体切割磁感线时会有电磁感应现象，其机理可由洛伦兹力解释

物理学家法拉第在研究电磁学时，亲手做过许多实验，如右图所示的就是著名的电磁旋转实验．它的现象是：如果载流导线附近只有磁铁的一个极，磁铁就会围绕导线旋转；反之，载流导线也会围绕单独的某一磁极旋转．这一装置实际上就是最早的电动机．图中a是可动磁铁，b是固定导线，c是可动导线，d是固定磁铁．图中黑色部分表示汞，下部接在电源上，则从上向下看，a、c旋转的情况是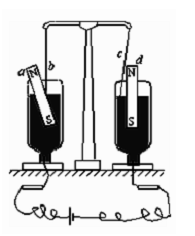

A．a顺时针，c逆时针．	B．a逆时针，c顺时针．
C．a逆时针，c逆时针．	D．a顺时针，c顺时针．

用单位长度质量为m、单位长度电阻为r的薄金属条制成边长为L的闭合正方形框。如图所示，金属方框水平放在磁极的狭缝间，方框平面与磁场方向平行。设匀强磁场仅存在于异名相对磁极的狭缝间，其它地方的磁场忽略不计。可认为方框的边和边都处在磁极之间。将方框从静止开始释放，在下落过程中其平面始终保持水平（不计空气阻力）。方框下落的最大速度为v_m。

（1）求磁极狭缝间磁感应强度B的大小（设磁场区域在竖直方向足够长）；
（2）当方框下落的加速度为时，求方框的发热功率P；
（3）已知方框下落时间为t时，下落高度为h，其速度为v_t（v_t<v_m）。若在同一时间t内，方框内产生的热量与某恒定电流I₀在该框内产生的热量相同，求恒定电流I₀的表达式。

如图所示，正方形导线框ABCD之边长l=10cm，质量m=50g，电阻R=0.1Ω。让线框立在地面上，钩码质量m′=70g，用不可伸长的细线绕过两个定滑轮，连接线框AB边的中点和钩码，线框上方某一高度以上有匀强磁场B=1.0T。当钩码由图示位置被静止释放后，线框即被拉起，上升到AB边进入磁场时就作匀速运动。细绳质量、绳与滑轮间的摩擦和空气阻力均不计，g取10m/s²，求：

（1）线框匀速进入磁场时其中的电流。
（2）线框全部进入磁场所用的时间。
（3）在线框匀速进入磁场的过程中线框产生的电能占钩码损失的机械能的百分比。
（4）线框从图示位置到AB边恰好进入磁场时上升的高度。

如图所示，闭合的矩形导体线圈abcd在匀强磁场中绕垂直于磁感线的对称轴OO′匀速转动，沿着OO′方向观察，线圈沿逆时针方向转动。已知匀强磁场的磁感强度为B，线圈匝数为n，ab边的边长为l₁，ad边的边长为l₂，线圈电阻为R，转动的角速度为，则当线圈转至图示位置时           （     ）

A．线圈中感应电流的方向为abcda

B．线圈中的感应电动势为

C．穿过线圈磁通量随时间的变化率最大

D．线圈ad边所受安培力的大小为

如图所示，平行光滑导轨MN和M′N′置于水平面内，导轨间距为l，电阻可以忽略不计。导轨的左端通过电阻忽略不计的导线接一阻值为R的定值电阻。金属棒ab垂直于导轨放置，其阻值也为R。导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。当金属棒ab在导轨上以某一速度向右做匀速滑动时，定值电阻R两端的电压为U。
（1）判断M和M′哪端电势高？
（2）求金属棒ab在导轨上滑动速度的大小。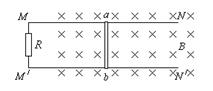

用电阻为18 Ω的均匀导线弯成如图中直径D ="0.80" m的封闭金属圆环，环上AB弧所对应的圆心角为60^º，将圆环垂直于磁感线方向固定在磁感应强度B ="0.50" T的匀强磁场中，磁场方向垂直于纸面向里．一根每米电阻为1.25 Ω的直导线PQ，沿圆环平面向左以3.0 m/s的速度匀速滑行（速度方向与PQ垂直），滑行中直导线与圆环紧密接触（忽略接触处的电阻），当它通过环上A、B位置时，求：
（1）直导线AB段产生的感应电动势，并指明该段直导线中电流的方向．
（2）此时圆环上发热损耗的电功率．

在图2所示的四个情景中，虚线上方空间都存在方向垂直纸面向里的匀强磁场。A、B中的导线框为正方形，C、D中的导线框为直角扇形。各导线框均绕轴O在纸面内匀速转动，转动方向如箭头所示，转动周期均为T。从线框处于图示位置时开始计时，以在OP边上从P点指向O点的方向为感应电流i的正方向。则在图2所示的四个情景中，产生的感应电流i随时间t的变化规律如图1所示的是

如图所示，在磁感应强度为B=2T，方向垂直纸面向里的匀强磁场中，有一个由两条曲线状的金属导线及两电阻（图中黑点表示）组成的固定导轨，两电阻的阻值分别为R₁=3Ω、R₂=6Ω，两电阻的体积大小可忽略不计，两条导线的电阻忽略不计且中间用绝缘材料隔开，导轨平面与磁场垂直（位于纸面内），导轨与磁场边界（图中虚线）相切，切点为A，现有一根电阻不计、足够长的金属棒MN与磁场边界重叠，在A点对金属棒MN施加一个方向与磁场垂直、位于导轨平面内的并与磁场边界垂直的拉力F，将金属棒MN以速度v=5m／s匀速向右拉，金属棒MN与导轨接触良好，以切点为坐标原点，以F的方向为正方向建立x轴，两条导线的形状符合曲线方程 m，求：
（1）推导出感应电动势e的大小与金属棒的位移x的关系式．
（2）整个过程中力F所做的功．
（3）从A到导轨中央的过程中通过R₁的电荷量．

如图所示，矩形闭合线圈放置在水平薄板上，有一块蹄形磁铁如图所示置于平板的正下方（磁极间距略大于矩形线圈的宽度）当磁铁匀速向右通过线圈时，线圈仍静止不动，那么线圈受到薄板的摩擦力方向是        （   ）

A．一直向左

B．一直向右

C．先向左，后向右

D．先向右，后向左

如图所示，两足够长平行金属导轨固定在水平面上，匀强磁场方向垂直导轨平面向下，金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动，两金属棒ab、cd的质量之比为2 ：1,用一沿导轨方向的恒力F水平向右拉金属棒cd，经过足够长时间以后                               （   ）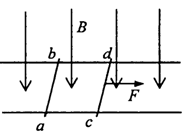

A．金属棒ab、cd都做匀速运动

B．金属棒ab上的电流方向是由b向a

C．金属棒cd所受安培力的大小等于2F／3

D．两金属棒间距离保持不变