如图所示，一个矩形线圈，在匀强磁场中绕一固定轴做匀速转动，
当线圈处于图中所示位置时（ ）
| A．磁通量最小，磁通量的变化率和感应电动势最大 |
| B．磁通量、磁通量的变化率和感应电动势都最大 |
| C．磁通量和磁通量的变化率最大，感应电动势最小 |
| D．磁通量、磁通量的变化率和感应电动势都最小 |
将面积为0.50m2的线圈放在磁感应强度为2.0×10－3T的匀强磁场中，线圈平面与磁场方向垂直，则穿过线圈的磁通量是( )
| A．1.0×10－3Wb | B．0.50×10－3Wb | C．0.25×10－3Wb | D．0 |
．(2009·广东模拟)如图所示，水平放置的扁平条形磁铁，在磁铁的左端正上方有一金属线框，线框平面与磁铁垂直，当线框从左端正上方沿水平方向平移到右端正上方的过程中，穿过它的磁通量的变化情况是 ( )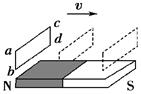
| A．先减小后增大 | B．始终减小 |
| C．始终增大 | D．先增大后减小 |
．关于电磁感应现象中，通过线圈的磁通量与感应电动势关系正确的是
| A．穿过线圈的磁通量越大，感应电动势越大 |
| B．穿过线圈的磁通量为零，感应电动势一定为零 |
| C．穿过线圈的磁通量变化越大，感应电动势越大 |
| D．穿过线圈的磁通量变化越快，感应电动势越大 |
如图所示，闭合矩形线框abcd位于磁感应强度为B的匀强磁场中，ad边位于磁场边缘，线框平面与磁场垂直，ab、ad边长分别用L1、L2表示，若把线圈沿v方向匀速拉出磁场所用时间为△t，则通过线框导线截面的电量是( )
A． |
B． |
C． |
D．BL1L2 |
如图所示，一个面积为S的矩形导线框abcd，在匀强磁场中，磁场的磁感应强度为B，方向与ad边垂直并与线框平面成370角，水平轴oo’， o、o’分别是ab和cd边的中点。现将线框绕oo’ 逆时针转过1800。在这一过程中，导线框的磁通量变化量大小是 (sin370=0.6 cos370="0.8)" ( )
| A．2BS | B．1.2BS | C．1.6BS | D．0 |
如图所示，将一条形磁铁沿闭合线圈中心轴线以不同速度匀速穿过线圈，第一次所用时间为t1，第二次所用时间为t2。则
| A．两次通过电阻R的电荷量相同 |
| B．两次电阻R中产生的热量相同 |
| C．每次电阻R中通过的电流方向保持不变 |
| D．磁铁处于线圈左侧时受到的磁场力向左，处于线圈右侧时受到的磁场力向右 |
如图所示，套在条形磁铁外的三个线圈，其面积S1＞S2= S3，且 “3”线圈在磁铁的正中间。设各线圈中的磁通量依次为φ1、φ2、φ3则它们的大小关系是[ ]
| A．φ1>φ2>φ3 | B．φ1>φ2=φ3 | C．φ1<φ2<φ3 | D．φ1<φ2=φ3 |
有一个金属丝圆环，圆面积为S，电阻为r，放在磁场中，让磁感线垂直地穿过圆环所在平面。在△t时间内，磁感应强度的变化为△B，通过金属丝横截面的电量q与下面哪个量的大小无关
| A．时间△t | B．圆面积S | C．金属丝圆环电阻 |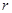
D．磁感应强度变化△B |
如图所示，两块水平放置的金属板距离为d，用导线、电键K与一个n匝的线圈连接，线圈置于方向竖直向上的均匀变化的磁场B中。两板间放一台小压力传感器，压力传感器上表面绝缘，在其上表面静止放置一个质量为m、电量为+q的小球。K断开时传感器上有示数，K闭合时传感器上的示数变为原来的一半。则线圈中磁场B的变化情况和磁通量变化率分别是 （ ）
A．正在增加， |
B．正在增加， |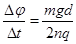
| C．正在减弱， |
D．正在减弱， |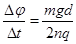
平行闭合线圈的匝数为n，所围面积为S，总电阻为R，在
时间内穿过每匝线圈的磁通量变化为
，则通过导线某一截面的电荷量为
A． |
B． |
C． |
D． |
某线圈在匀强磁场中匀速转动，穿过它的磁通量φ随时间的变化规律可用右图表示，则（ ）
| A．t1和t2时刻，穿过线圈磁通量的变化率最大 |
| B．t2时刻，穿过线圈的磁通量变化率为零 |
| C．t3时刻，线圈中的感应电动势为零 |
| D．t4时刻，线圈中的感应电动势达最大值 |
如图所示，在水平匀强磁场中数值放置一矩形线圈，线圈平面与磁场垂直，线圈绕其底边转过90°至水平位置的过程中，穿过线圈的磁通量的变化情况是（ ）
| A．变大 | B．变小 | C．先变大后变小 | D．先变小后变大 |
下列说法正确的是（ ）
| A．电路中如果存在感应电动势，那么就一定存在感应电流 |
| B．只要电路的一部分做切割磁感线运动，电路中就一定有感应电流 |
| C．穿过电路的磁通量越大，电路中的感应电流一定越大 |
| D．穿过电路的磁通量变化越快，电路中产生的感应电动势越大 |
粤公网安备 44130202000953号
的时刻，线框中的感应电动势为
的时刻，线框中的感应电动势为
