如图所示,在绝缘水平面上固定两个等量同种电荷P、Q,在PQ连线上的M点由静止释放一带电滑块,则滑块会由静止开始一直向右运动到PQ连线上的另一点N而停下,则以下说法正确的是( )

| A.滑块受到的电场力可能是先减小后增大 |
| B.滑块的电势能一直减小 |
| C.滑块的动能与电势能之和可能保持不变 |
| D.PM间距一定小于QN间距 |
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图。在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球。设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力)。则有
| A.Ta =" Tb" =" Td" = Tc,Ea > Eb =" Ed" > Ec |
| B.Ta =" Tb" =" Td" = Tc,Ea =" Eb" =" Ed" = Ec |
| C.Ta < Tb =" Td" < Tc,Ea > Eb =" Ed" > Ec |
| D.Ta < Tb =" Td" < Tc,Ea =" Eb" =" Ed" = Ec |
劲度系数为k的轻质弹簧,一端系在竖直放置、半径为R的光滑圆环顶点P,另一端连接一套在圆环上且质量为m的小球.开始时小球位于A点,此时弹簧处于原长且与竖直方向的夹角为45°,之后小球由静止沿圆环下滑,小球运动的最低点B时的速率为v,此时小球与圆环之间的压力恰好为零,已知重力加速度为g.下列分析正确的是( )
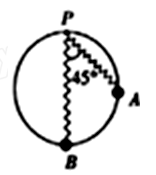
| A.轻质弹簧的原长为R |
B.小球过B点时,所受的合力为 |
| C.小球从A到B的过程中,重力势能转化为弹簧的弹性势能 |
D.小球运动到B点时,弹簧的弹性势能为mgR-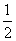 mv2 mv2 |
带式传送机是在一定的线路上连续输送物料的搬运机械,又称连续输送机.如图所示,一条足够长的浅色水平传送带自左向右匀速运行.现将一个木炭包无初速度地放在传送带上,木炭包在传送带上将会留下一段黑色的径迹.下列说法正确的是
| A.黑色的径迹将出现在木炭包的左侧 |
| B.木炭包的质量越大,径迹的长度越短 |
| C.木炭包与传送带间动摩擦因数越大,径迹的长度越短 |
| D.传送带运动的速度越大,径迹的长度越短 |
如图所示,质量相等的A、B小物块用轻弹簧相连,用细线把A悬挂在天花板上,B放在水平面,静止时,B对水平面的压力刚好为零。忽略空气阻力,剪断A上的细线之后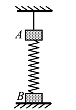
A.A向下运动过程中,加速度先减小后增大
B.A向下运动过程中,在弹簧处于原长时速度达到最大
C.A运动到最低点时,地面对B的支持力等于A、B的重力之和
D.A运动到最低点时,弹簧的弹性势能与细绳剪断前相等
如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法正确的是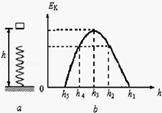
| A.小物体下降至高度h3时,弹簧形变量为0 |
| B.小物体下落至高度h5时,加速度为0 |
C.小物体从高度h2下降到h4,弹簧的弹性势能增加了 |
| D.小物体从高度h1下降到h5,弹簧的最大弹性势能为mg(h1-h5) |
如图所示,质量为m的物块与水平转台之间的动摩擦因数为μ,物块与转台转轴相距R,物块随转台由静止开始转动并计时,在t1时刻转速达到n,物块即将开始滑动.保持转速n不变,继续转动到t2时刻.则( )

| A.在0~t1时间内,摩擦力做功为零 |
| B.在t1~t2时间内,摩擦力做功为2μmgR |
| C.在0~t1时间内,摩擦力做功为2μmgR |
| D.在0~t1时间内,摩擦力做功为μmgR |
如图所示,轻质弹簧的一端与固定的竖直板P拴接,另一端与物体A相连,物体A静止于光滑水平桌面上,右端接一细线,细线绕过光滑的定滑轮与物体B相连.开始时用手托住B,让细线恰好伸直,然后由静止释放B,直至B获得最大速度.下列有关该过程的分析正确的是 ( )

| A.B物体的机械能一直减小 |
| B.B物体的动能的增加量等于它所受重力与拉力做的功之和 |
| C.B物体机械能的减少量等于弹簧的弹性势能的增加量 |
| D.细线拉力对A物体做的功等于A物体与弹簧所组成的系统机械能的增加 |
如图所示,轻质弹簧竖直放置在水平地面上,它的正上方有一金属块从高处自由下落,从金属块自由下落到第一次速度为零的过程中( )
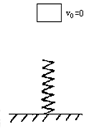
| A.弹力从没做正功 |
| B.重力先做正功,后做负功 |
| C.金属块的动能最大时,弹簧的弹性势能为零 |
| D.金属块的动能为零时,弹簧的弹性势能最大 |
如图所示,倾角θ=30°的固定斜面上固定着挡板,轻弹簧下端与挡板相连,弹簧处于原长时上端位于D点。用一根不可伸长的轻绳通过轻质光滑定滑轮连接物体A和B,使滑轮左侧绳子始终与斜面平行,初始时A位于斜面的C点,C、D两点间的距离为L。现由静止同时释放A、B,物体A沿斜面向下运动,将弹簧压缩到最短的位置为E点,D.E两点间距离为 。若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数
。若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数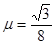 ,不计空气阻力,重力加速度为g。整个过程中,轻绳始终处于伸直状态,则( )
,不计空气阻力,重力加速度为g。整个过程中,轻绳始终处于伸直状态,则( )
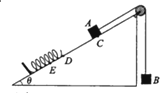
A.A在从C至E的过程中,先做匀加速运动,后做匀减速运动
B.A在从C至D的过程中,加速度大小为
C.弹簧的最大弹性势能为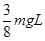
D.弹簧的最大弹性势能为
如图甲所示,轻弹簧竖直固定在水平面上.一质量为m=0.2kg的小球,从弹簧上端某高度处自由下落,从它接触弹簧到弹簧压缩至最短的过程中(弹簧在弹性限度内),其速度u和弹簧压缩量△x之间的函数图象如图乙所示,其中A为曲线的最高点.小球和弹簧接触瞬间机械能损失不计,g取10 m/s2,则下列说法正确的是( )
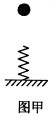
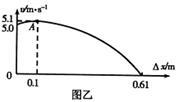
| A.小球刚接触弹簧时加速度最大 |
| B.从接触弹簧到压缩至最短的过程中,弹簧的弹性势能先增大后减小 |
| C.从接触弹簧到压缩至最短的过程中,小球的机械能守恒 |
| D.该弹簧的劲度系数为20.0 N/m |
如图所示,倾斜的传送带保持静止,一木块从顶端以一定的初速度匀加速下滑到底端,如果让传送带沿图中虚线箭头所示的方向匀速运动,同样的木块从顶端以同样的初速度下滑到底端的过程中,与传送带保持静止时相比
| A.木块在滑到底端的过程中,运动时间将变长 |
| B.木块在滑到底端的过程中,木块克服摩擦力所做功不变 |
| C.木块在滑到底端的过程中,动能的增加量减小 |
| D.木块在滑到底端的过程中,系统产生的内能减小 |
如图所示,竖直放置的轻弹簧上端与质量为3kg的物块B相连接,另一个质量为1kg的物块A放在B上.先向下压A,然后释放,A、B共同向上运动一段后将分离,分离后A又上升了0.2m到达最高点,此时B的速度方向向下,且弹簧恰好为原长.从A、B分离到A上升到最高点的过程中,弹簧弹力对B做的功及弹簧回到原长时B的速度大小分别是(g=10m/s2)( )
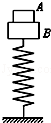
A.12 J,2m/s B.0,2m/s C.0,0 D.4J,2m/s
升降机底板上放一质量为10kg的物体,物体随升降机由静止开始竖直上升6m时,速度达到10m/s,则此过程中(重力加速度g取10m/s2)( )
| A.合外力对物体做功600 J | B.物体的重力势能增加600 J |
| C.升降机对物体做功500 J | D.物体的机械能增加1100 J |