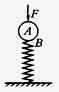
如图所示,轻放在竖直轻弹簧上端的小球A,在竖直向下的恒力F的作用下,弹簧被压缩到B点。现突然撤去力F,小球将在竖直方向上开始运动,若不计空气阻力,则下列中说法正确的是( )
| A.撤去F后小球、地球、弹簧构成的系统机械能守恒 |
| B.小球在上升过程中,动能先增大后减小 |
| C.小球在上升过程中,弹性势能先减小后增大 |
| D.小球在上升过程中,弹簧的形变量恢复到最初(指撤去力F的瞬间)的一半时,小球的动能最大 |
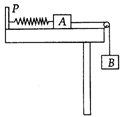
如图所示,轻质弹簧的一端与固定的竖直板P栓接,另一端与物体A相连,物体A静止与光滑水平桌面上,右端接一细线,细线绕过光滑的轻质定滑轮与物体B相连,开始时用手托住B,让细线恰好伸直,然后由静止释放B,直至B获得最大速度,下列有关该过程的分析正确的是( )
| A.B物体的机械能一直在增大 |
| B.B物体的动能的增加量等于它所受重力与拉力做的功之和 |
| C.B物体机械能的减小量等于弹簧的弹性势能的增加量 |
| D.细线拉力对A做的功等于A物体与弹簧所组成的系统机械能的增加量 |
某同学利用下述装置对轻质弹簧的弹性势能进行探究,一轻质弹簧放置在光滑水平桌面上,弹簧左端固定,右端与一小球接触而不固连:弹簧处于原长时,小球恰好在桌面边缘,如图(a)所示。向左推小球,使弹黄压缩一段距离后由静止释放:小球离开桌面后落到水平地面。通过测量和计算,可求得弹簧被压缩后的弹性势能。
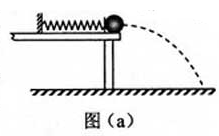
回答下列问题:
(1)本实验中可认为,弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等。已知重力加速度大小为g。为求得Ek,至少需要测量下列物理量中的 (填正确答案标号)。
| A.小球的质量m |
| B.小球抛出点到落地点的水平距离s |
| C.桌面到地面的高度h |
| D.弹簧的压缩量△x |
E.弹簧原长l0
(2)用所选取的测量量和已知量表示Ek,得Ek= 。
(3)图(b)中的直线是实验测量得到的s-△x图线。从理论上可推出,如果h不变.m增加,s—△x图线的斜率会 (填“增大”、“减小”或“不变”):如果m不变,h增加,s—△x图线的斜率会 (填“增大”、“减小”或“不变”)。由图(b) 中给出的直线关系和Ek的表达式可知,Ep与△x的 次方成正比。

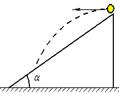
如图所示,有一个足够长的斜坡,倾角为α=30º。一个小孩在做游戏时,从该斜坡顶端将一足球沿水平方向水平踢出去,已知足球被踢出时的初动能为9J,则该足球第一次落在斜坡上时的动能为
| A.12J | B.21J | C.27J | D.36J |
如图所示,置于足够长斜面上的盒子闪为放有光滑球B,B洽与盒子前、后壁接触,斜面光滑且固定于水平地面上.一轻质弹簧的一端与固定在斜面上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放,则从释放盒子直至其获得最大速度的过程中( )

| A.弹簧的弹性势能一直减小直至为零 |
| B.A对B做的功等于B机械能的增加量 |
| C.弹簧弹性势能的减小量等于A和B机械能的增加量 |
| D.A所受重力和弹簧弹力做功的代数和小于A动能的增加量 |
如图所示,质量为m的物块与水平转台之间的动摩擦因数为μ,物块与转台转轴相距R,物块随转台由静止开始转动并计时,在t1时刻转速达到n,物块即将开始滑动.保持转速n不变,继续转动到t2时刻.则( )

| A.在0~t1时间内,摩擦力做功为零 |
| B.在t1~t2时间内,摩擦力做功为2μmgR |
| C.在0~t1时间内,摩擦力做功为2μmgR |
| D.在0~t1时间内,摩擦力做功为μmgR |
如图是为了检验某种防护罩承受冲击力的装置,M是半径为R=1.0m的固定于竖直平面内的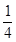 光滑圆弧轨道,轨道上端切线水平。N为待检验的固定曲面,该曲面在竖直面内的截面为半径
光滑圆弧轨道,轨道上端切线水平。N为待检验的固定曲面,该曲面在竖直面内的截面为半径 的
的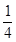 圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点。M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量m=0.01kg的小钢珠,假设某次发射的钢珠沿轨道恰好能经过M的上端点,水平飞出后落到曲面N的某一点上,取g=10m/s2。求:
圆弧,圆弧下端切线水平且圆心恰好位于M轨道的上端点。M的下端相切处放置竖直向上的弹簧枪,可发射速度不同的质量m=0.01kg的小钢珠,假设某次发射的钢珠沿轨道恰好能经过M的上端点,水平飞出后落到曲面N的某一点上,取g=10m/s2。求: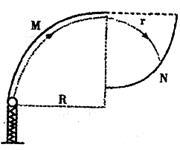
(1)发射该钢球前,弹簧的弹性势能EP多大?
(2)钢珠从M圆弧轨道最高点飞出至落到圆弧N上所用的时间是多少(结果保留两位有效数字)?
如图所示,质量相等的A、B小物块用轻弹簧相连,用细线把A悬挂在天花板上,B放在水平面,静止时,B对水平面的压力刚好为零。忽略空气阻力,剪断A上的细线之后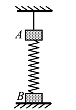
A.A向下运动过程中,加速度先减小后增大
B.A向下运动过程中,在弹簧处于原长时速度达到最大
C.A运动到最低点时,地面对B的支持力等于A、B的重力之和
D.A运动到最低点时,弹簧的弹性势能与细绳剪断前相等
如图所示,将一轻弹簧下端固定在倾角为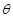 的粗糙斜面底端,弹簧处于自然状态时上端位于A点.质量为m的物体从斜面上的B点静止下滑,与弹簧发生相互作用后,最终停在斜面上.下列说法正确的是( )
的粗糙斜面底端,弹簧处于自然状态时上端位于A点.质量为m的物体从斜面上的B点静止下滑,与弹簧发生相互作用后,最终停在斜面上.下列说法正确的是( )
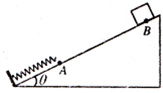
| A.物体最终将停在A点 |
| B.物体第一次反弹后不可能到达B点 |
| C.整个过程中重力势能的减少量大于克服摩擦力做的功 |
| D.整个过程中物体的最大动能小于弹簧的最大弹性势能 |
如图所示,倾角θ=30°的固定斜面上固定着挡板,轻弹簧下端与挡板相连,弹簧处于原长时上端位于D点。用一根不可伸长的轻绳通过轻质光滑定滑轮连接物体A和B,使滑轮左侧绳子始终与斜面平行,初始时A位于斜面的C点,C、D两点间的距离为L。现由静止同时释放A、B,物体A沿斜面向下运动,将弹簧压缩到最短的位置为E点,D.E两点间距离为 。若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数
。若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数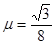 ,不计空气阻力,重力加速度为g。整个过程中,轻绳始终处于伸直状态,则( )
,不计空气阻力,重力加速度为g。整个过程中,轻绳始终处于伸直状态,则( )
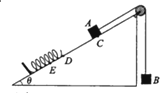
A.A在从C至E的过程中,先做匀加速运动,后做匀减速运动
B.A在从C至D的过程中,加速度大小为
C.弹簧的最大弹性势能为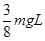
D.弹簧的最大弹性势能为
劲度系数为k的轻质弹簧,一端系在竖直放置、半径为R的光滑圆环顶点P,另一端连接一套在圆环上且质量为m的小球.开始时小球位于A点,此时弹簧处于原长且与竖直方向的夹角为45°,之后小球由静止沿圆环下滑,小球运动的最低点B时的速率为v,此时小球与圆环之间的压力恰好为零,已知重力加速度为g.下列分析正确的是( )
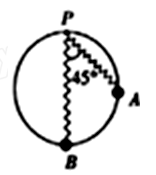
| A.轻质弹簧的原长为R |
B.小球过B点时,所受的合力为 |
| C.小球从A到B的过程中,重力势能转化为弹簧的弹性势能 |
D.小球运动到B点时,弹簧的弹性势能为mgR-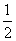 mv2 mv2 |
如图所示,一物块与水平方向成θ角的拉力F作用下,沿水平面向右运动一段距离x,在此过程中,拉力F对物块所做的功为( )

A. |
B.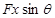 |
C. |
D.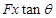 |
如图a所示,小物体从竖直弹簧上方离地高h1处由静止释放,其动能Ek与离地高度h的关系如图b所示.其中高度从h1下降到h2,图象为直线,其余部分为曲线,h3对应图象的最高点,轻弹簧劲度系数为k,小物体质量为m,重力加速度为g.以下说法正确的是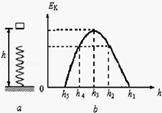
| A.小物体下降至高度h3时,弹簧形变量为0 |
| B.小物体下落至高度h5时,加速度为0 |
C.小物体从高度h2下降到h4,弹簧的弹性势能增加了 |
| D.小物体从高度h1下降到h5,弹簧的最大弹性势能为mg(h1-h5) |
如图所示,光滑水平地面上有一质量为2m的物体A,A以水平速度v0向右运动。在A的右侧静止一质量为m的物体B,B的左侧与一轻弹簧固定相连,B的右侧有一固定的挡板,B与挡板的碰撞是弹性的,在弹簧与A第一次相互作用的过程中,B不会碰到挡板,求: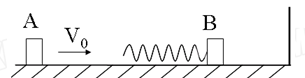
(1)A与弹簧第一次相互作用过程中,弹簧的最大弹性势能大小。
(2)弹簧与A第二次相互作用后A的速度大小。
如图所示,ABCD为固定在竖直平面内的轨道,AB段光滑水平,BC段为光滑圆弧,对应的圆心角θ=37º,半径r=2.5m,CD段平直倾斜且粗糙,各段轨道均平滑连接,倾斜轨道所在区域有场强大小为E=2×105 N/C、方向垂直于斜轨向下的匀强电场。质量m=5×10-2 kg、电荷量q=+1×10-6 C的小物体(视为质点)被弹簧枪发射后,沿水平轨道向左滑行,在C点以速度v0=3 m/s冲上斜轨。以小物体通过C点时为计时起点,0.1s以后,场强大小不变,方向反向。已知斜轨与小物体间的动摩擦因数μ=0.25。设小物体的电荷量保持不变,取g=10 m/s2,sin37º=0.6,cos37º=0.8。

(1)求弹簧枪对小物块所做的功;
(2)在斜轨上小物体能到达的最高点为P,求CP的长度。